题目内容
18. 已知椭圆 C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的两个焦点F1,F2,动点P在椭圆上,且使得∠F1PF2=90°的点P恰有两个,动点P到焦点F1的距离的最大值为2+$\sqrt{2}$.
已知椭圆 C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的两个焦点F1,F2,动点P在椭圆上,且使得∠F1PF2=90°的点P恰有两个,动点P到焦点F1的距离的最大值为2+$\sqrt{2}$.(Ⅰ)求椭圆C1的方程;
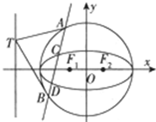
(Ⅱ)如图,以椭圆C1的长轴为直径作圆C2,过直线x=-2$\sqrt{2}$上的动点T作圆C2的两条切线,设切点分别为A,B,若直线AB与椭圆C1交于不同的两点C,D,求弦|CD|长的取值范围.
分析 (I)利用条件推出$b=c,a=\sqrt{2}c$;动点P到焦点F1的距离的最大值为$2+\sqrt{2}$,可得$a+c=2+\sqrt{2}$,求出a、c、b,即可求出椭圆方程.
(II)设直线$x=-2\sqrt{2}$上动点T的坐标为$(-2\sqrt{2},t)$,设A(x1,y1),B(x2,y2),求出直线AT的方程为x1x+y1y=4,直线BT的方程为x2x+y2y=4,通过$\left\{{\begin{array}{l}{-2\sqrt{2}{x_1}+t{y_1}=4}\\{-2\sqrt{2}{x_2}+t{y_2}=4}\end{array}}\right.$,得到直线AB的方程,联立直线与椭圆方设C(x3,y3),D(x4,y4).利用韦达定理求解|CD|,然后求出范围即可.
解答 解:(I)由使得∠F1PF2=90°的点P恰有两个可得$b=c,a=\sqrt{2}c$;动点P到焦点F1的距离的最大值为$2+\sqrt{2}$,可得$a+c=2+\sqrt{2}$,即$a=2,c=\sqrt{2}$,
所以椭圆C1的方程是$\frac{x^2}{4}+\frac{y^2}{2}=1$…(4分)
(II)圆C2的方程为x2+y2=4,设直线$x=-2\sqrt{2}$上动点T的坐标为$(-2\sqrt{2},t)$设A(x1,y1),B(x2,y2),则直线AT的方程为x1x+y1y=4,直线BT的方程为x2x+y2y=4,又$(-2\sqrt{2},t)$在直线AT和BT上,即$\left\{{\begin{array}{l}{-2\sqrt{2}{x_1}+t{y_1}=4}\\{-2\sqrt{2}{x_2}+t{y_2}=4}\end{array}}\right.$,
故直线AB的方程为$-2\sqrt{2}x+ty=4$…(6分)
联立$\left\{{\begin{array}{l}{-2\sqrt{2}x+ty=4}\\{\frac{x^2}{4}+\frac{y^2}{2}=1}\end{array}}\right.$,消去x得(t2+16)y2-8yt-16=0,设C(x3,y3),D(x4,y4).
则${y_3}+{y_4}=\frac{8t}{{{t^2}+16}},{y_3}{y_4}=\frac{-16}{{{t^2}+16}}$,…(8分)
从而$|{CD}|=\sqrt{1+\frac{t^2}{8}}|{{y_1}-{y_2}}|=\frac{{4({t^2}+8)}}{{({t^2}+16)}}$…(10分)
=$4+\frac{-32}{{t}^{2}+16}$,
又t2+16≥16,从而$-2≤\frac{-32}{{t}^{2}+16}<0$,所以|CD|∈[2,4)…(12分)
点评 本题考查椭圆方程的求法,直线与椭圆位置关系的综合应用,考查分析问题解决问题的能力.转化思想的应用,是难度比较大的题目.

| A. | 直线y=0对称 | B. | 直线x=0对称 | C. | 直线y=1对称 | D. | 直线x=1对称 |
| A. | (0,1) | B. | (1,2) | C. | (2,e) | D. | (3,4) |
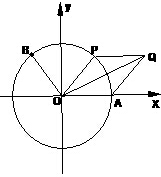 如图,点A是单位圆与x轴正半轴的交点,B(-$\frac{3}{5}$,$\frac{4}{5}$).
如图,点A是单位圆与x轴正半轴的交点,B(-$\frac{3}{5}$,$\frac{4}{5}$). 甲、乙两人在9天每天加工零件的个数用茎叶图表示如图,则这9天甲、乙加工零件个数的中位数之和为91.(考点:茎叶图与中位数综合)
甲、乙两人在9天每天加工零件的个数用茎叶图表示如图,则这9天甲、乙加工零件个数的中位数之和为91.(考点:茎叶图与中位数综合)