题目内容
9.甲和乙等五名志愿者被随机地分到A、B、C三个不同的岗位服务,每个岗位至少有一名志愿者.若甲和乙不在同一岗位服务,则不同的分法有138种.(用数字作答)分析 利用间接法由题意得,再排除甲乙两人在同一岗位的分配方法,问题得以解决.
解答 解:利用间接法由题意得,五名志愿者被随机地分到A,B,C三个不同的岗位,每个岗位至少有一名志愿者人,
可以有一个岗位3人,其余各1人,有C53A33=60种,也可能有一个岗位1人,其余各2人,有3C52C32=90种,
要满足甲、乙被同时安排在A岗位,则相当于把其余3人分到A,B,C岗位,有A33+C32A22=12种,
故甲和乙不在同一岗位服务,则不同的分法有60+90-12=138.
故答案为:138.
点评 本题主要考查了排列组合中的分配问题,关键是如何分组,属于中档题

练习册系列答案
相关题目
20.以下是某个几何体的三视图(单位:cm),则该几何体的体积是( )
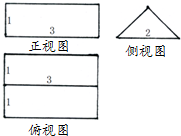

| A. | 2cm3 | B. | 3cm3 | C. | 4cm3 | D. | 5cm3 |
4.对于函数f(x)=eax-lnx,(a是实常数),下列结论正确的一个是( )
| A. | a=1时,B有极大值,且极大值点(1,3) | |
| B. | a=2时,A有极小值,且极小值点x0∈(0,$\frac{1}{4}$) | |
| C. | a=$\frac{1}{2}$时,D有极小值,且极小值点x0∈(1,2) | |
| D. | a<0时,C有极大值,且极大值点x0∈(-∞,0) |
1.已知i是虚数单位,则复数z=i2015的虚部是( )
| A. | 0 | B. | -1 | C. | 1 | D. | -i |
19.将9个相同的小球放入3个不同的盒子,要求每个盒子中至少有一个小球,且每个盒子里的小球个数都不相同,则不同的放法种数为( )
| A. | 12 | B. | 15 | C. | 18 | D. | 21 |
 如图,已知 AF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=CD=2,AB=4.
如图,已知 AF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=CD=2,AB=4.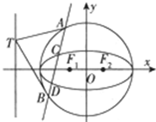 已知椭圆 C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的两个焦点F1,F2,动点P在椭圆上,且使得∠F1PF2=90°的点P恰有两个,动点P到焦点F1的距离的最大值为2+$\sqrt{2}$.
已知椭圆 C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的两个焦点F1,F2,动点P在椭圆上,且使得∠F1PF2=90°的点P恰有两个,动点P到焦点F1的距离的最大值为2+$\sqrt{2}$.