题目内容
10.对于映射f:A→B,若A中的不同元素有不同的象,且B中的每一个元素都有原象,则称f:A→B为一一映射,若存在对应关系Φ,使A到B成为一一映射,则称A到B具有相同的势,给出下列命题:①A是奇数集,B是偶数集,则A和B具有相同的势;
②A是平面直角坐标系内所有点形成的集合,B是复数集,则A和B不具有相同的势;
③若区间A=(-1,1),B=R,则A和B具有相同的势.
其中正确命题的序号是①③.
分析 对于①,根据奇数与偶数的定义,给出一个对应法则可验证①的正确性;
对②,根据复数的几何意义,可判断能否形成一一映射,来判断②是否正确;
对③,给出对应法则y=tan$\frac{π}{2}$x,可验证③的正确性.
解答 解:根据一一映射的定义,集合A={奇数}→B={偶数},不妨给出对应法则加1.则A→B是一一映射,故①正确;
对②设Z点的坐标(a,b),则Z点对应复数a+bi,a、b∈R,复合一一映射的定义,故②不正确;
对③,给出对应法则y=tan$\frac{π}{2}$x,对于A,B两集合可形成f:A→B的一一映射,则A、B具有相同的势;∴③正确.
故选:①③
点评 本题借助考查命题的真假判断,考查一一映射的定义,属于基础题型,考查考生对新定义题的理解与应用能力.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
20.以下是某个几何体的三视图(单位:cm),则该几何体的体积是( )
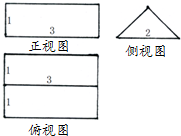

| A. | 2cm3 | B. | 3cm3 | C. | 4cm3 | D. | 5cm3 |
1.已知i是虚数单位,则复数z=i2015的虚部是( )
| A. | 0 | B. | -1 | C. | 1 | D. | -i |
5.双曲线$\frac{x^2}{{{m^2}-4}}+\frac{y^2}{m^2}$=1(m∈Z)的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 3 |
19.将9个相同的小球放入3个不同的盒子,要求每个盒子中至少有一个小球,且每个盒子里的小球个数都不相同,则不同的放法种数为( )
| A. | 12 | B. | 15 | C. | 18 | D. | 21 |
20.教室内有一把直尺,无论这把直尺怎样放置,在教室的地面上总能画出一条直线,使这条直线与直尺( )
| A. | 平行 | B. | 垂直 | C. | 异面 | D. | 相交 |
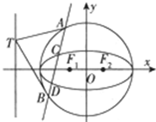 已知椭圆 C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的两个焦点F1,F2,动点P在椭圆上,且使得∠F1PF2=90°的点P恰有两个,动点P到焦点F1的距离的最大值为2+$\sqrt{2}$.
已知椭圆 C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的两个焦点F1,F2,动点P在椭圆上,且使得∠F1PF2=90°的点P恰有两个,动点P到焦点F1的距离的最大值为2+$\sqrt{2}$.