题目内容

3．函数f（x）=log2（x+2）-$\frac{3}{x}$（x＞0）的零点所在的大致区间是（　　）
A．（0，1）B．（1，2）C．（2，e）D．（3，4）

分析 分别求出f（1），f（2）的值，从而求出函数的零点所在的范围．

解答 解：∵f（1）=${log}_{2}^{3}$-3＜0，f（2）=${log}_{2}^{4}$-$\frac{3}{2}$=2-$\frac{3}{2}$＞0，
∴函数f（x）=log2（x+2）-$\frac{3}{x}$（x＞0）的零点所在的大致区间是（1，2），
故选：B．

点评 本题考察了函数的零点问题，根据零点定理求出即可，本题是一道基础题．

练习册系列答案
相关题目
13．在△ABC中，角A，B，C所对的边分别为a，b，c，且$2{cos^2}\frac{A-B}{2}cosB-sin（A-B）sinB+cos（A+C）=-\frac{1}{2}$
（Ⅰ）求A；
（Ⅱ）D为边BC上一点，BD=3DC，∠DAB=$\frac{π}{2}$，求tanC．
14．如图，已知 AF⊥平面ABCD，四边形ABEF为矩形，四边形ABCD为直角梯形，∠DAB=90°，AB∥CD，AD=AF=CD=2，AB=4．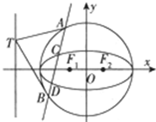
（I）求证：AC⊥平面BCE；
（II）求三棱锥E-BCF的体积．
11．已知f（x）=sinxsin（x+$\frac{π}{6}$），$x∈[-\frac{π}{3}，\frac{π}{3}]$，则f（x）的最小值为$\frac{\sqrt{3}-2}{4}$．
18．已知椭圆 C1：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的两个焦点F1，F2，动点P在椭圆上，且使得∠F1PF2=90°的点P恰有两个，动点P到焦点F1的距离的最大值为2+$\sqrt{2}$．
（Ⅰ）求椭圆C1的方程；
（Ⅱ）如图，以椭圆C1的长轴为直径作圆C2，过直线x=-2$\sqrt{2}$上的动点T作圆C2的两条切线，设切点分别为A，B，若直线AB与椭圆C1交于不同的两点C，D，求弦|CD|长的取值范围．
8．椭圆满足这样的光学性质：从椭圆的一个交点发射的光线，经椭圆反射后，反射光先经过椭圆的另一个交点，现设有一个水平放置的椭圆形台球盘，满足方程$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1，点A和B是它们的两个交点，当静止的小球放在点A处，从点A沿直线出发，经椭圆壁反弹后，再回到点A时，小球经过的路程是2或18或20．
15．数列{an}的前n项和记为 Sn，a1=2，an+1=Sn+n，等差数列{bn}的各项为正，其前n项和为Tn，且 T3=9，又 a1+b1，a2+b2，a3+b3成等比数列．
（Ⅰ）求{an}，{bn}的通项公式；
（Ⅱ）求证：当n≥2时，$\frac{1}{{{b}_{1}}^{2}}$+$\frac{1}{{{b}_{2}}^{2}}$+…+$\frac{1}{{{b}_{n}}^{2}}$＜$\frac{5}{4}$．
12．设椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左、右焦点分别是F1和F2，离心率e=$\frac{{\sqrt{2}}}{2}$，点F2到右准线l的距离为$\sqrt{2}$．
（Ⅰ）求a、b的值；
（Ⅱ）设M、N是右准线l上两动点，满足$\overrightarrow{{F_1}M}•\overrightarrow{{F_2}N}$=0．当|MN|取最小值时，求证：M，N两点关于x轴对称．
13．已知-$\frac{π}{2}＜α＜0＜β＜\frac{π}{2}$，cos（a-β）=$\frac{3}{5}$，sinβ=$\frac{5}{13}$，tanα=-$\frac{33}{56}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网