题目内容
【题目】下列4个命题:
(1)有两个面互相平行,其余四个面都是全等的等腰梯形的六面体是正四棱台;
(2)底面是正三角形,其余各面都是等腰三角形的棱锥是正三棱锥;
(3)各侧面都是等腰三角形的四棱锥是正四棱锥;
(4)底面是正三角形,相邻两侧而所成的二面角都相等的三棱锥是正三棱锥
中,假命题的个数为( ).
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】
对所给4个命题,各举反例如下:
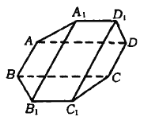
如图,两个全等的矩形同垂直于其中心连线,且对应边互相垂直(相当于一个矩形绕中心线旋转了![]() ),这个六面体不是正四梭台;
),这个六面体不是正四梭台;
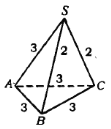
如图,三梭锥![]() 中,
中,![]() ,
,![]() ,这个三棱锥不是正三梭锥;
,这个三棱锥不是正三梭锥;
如图,四棱锥![]() 是圆锥的内接棱锥,其中
是圆锥的内接棱锥,其中![]() 是圆锥底面的直径,四梭锥
是圆锥底面的直径,四梭锥![]() 不是正四棱锥;
不是正四棱锥;

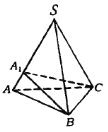
如图,正三棱锥![]() 中,棱
中,棱![]() 内存在点
内存在点![]() ,使
,使![]() ,则三棱锥
,则三棱锥![]() 不是正三棱锥.
不是正三棱锥.
选D.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案【题目】某便利店每天以每件5元的价格购进若干鲜奶,然后以每件10元价格出售,如果当天卖不完,剩下的鲜奶作餐厨垃圾处理.便利店记录了100天这种鲜奶的日需求量![]() (单位:件)如表所示:
(单位:件)如表所示:
日需求量n(件) | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
频数 | 10 | 20 | 16 | 16 | 15 | 12 | 11 |
以100天记录的各需求量的频率作为各需求量发生的概率.
(1)若便利店一天购进160件这种鲜奶,X表示当天的利润(单位:元),求X的分布列与数学期望及方差;
(2)若便利店一天购进160件或170件这种鲜奶,仅从获得利润大的角度考虑,你认为应购进160件还是170件?请说明理由.
【题目】某商场举行优惠促销活动,顾客仅可以从以下两种优惠方案中选择一种.
方案一:每满100元减20元;
方案二:满100元可抽奖一次.具体规则是从装有2个红球、2个白球的箱子随机取出3个球(逐个有放回地抽取),所得结果和享受的优惠如下表:(注:所有小球仅颜色有区别)
红球个数 | 3 | 2 | 1 | 0 |
实际付款 | 7折 | 8折 | 9折 | 原价 |
(1)该商场某顾客购物金额超过100元,若该顾客选择方案二,求该顾客获得7折或8折优惠的概率;
(2)若某顾客购物金额为180元,选择哪种方案更划算?
【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费
的包裹收费![]() 元;重量超过
元;重量超过![]() 的包裹,除
的包裹,除![]() 收费
收费![]() 元之外,超过
元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 计算)需再收
计算)需再收![]() 元.
元.
该公司将近![]() 天,每天揽件数量统计如下:
天,每天揽件数量统计如下:
包裹件数范围 |
|
|
|
|
|
包裹件数 (近似处理) |
|
|
|
|
|
天数 |
|
|
|
|
|
(1)某人打算将![]() ,
, ![]() ,
, ![]() 三件礼物随机分成两个包裹寄出,求该人支付的快递费不超过
三件礼物随机分成两个包裹寄出,求该人支付的快递费不超过![]() 元的概率;
元的概率;
(2)该公司从收取的每件快递的费用中抽取![]() 元作为前台工作人员的工资和公司利润,剩余的作为其他费用.前台工作人员每人每天揽件不超过
元作为前台工作人员的工资和公司利润,剩余的作为其他费用.前台工作人员每人每天揽件不超过![]() 件,工资
件,工资![]() 元,目前前台有工作人员
元,目前前台有工作人员![]() 人,那么,公司将前台工作人员裁员
人,那么,公司将前台工作人员裁员![]() 人对提高公司利润是否更有利?
人对提高公司利润是否更有利?
