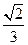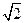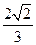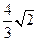题目内容
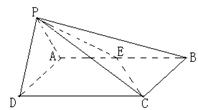
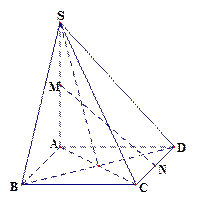
如图,在四棱锥P-ABCD中,底面ABCD是矩形,侧面PAD是正三角形且与底面ABCD垂直 ,E是AB的中点,PC与平面ABCD所成角为
,E是AB的中点,PC与平面ABCD所成角为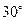 .
.
(1)求二面角P-CE-D的大小;
(2)当AD为多长时,点D到平面PCE 的距离为2.
 ,E是AB的中点,PC与平面ABCD所成角为
,E是AB的中点,PC与平面ABCD所成角为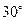 .
.
(1)求二面角P-CE-D的大小;
(2)当AD为多长时,点D到平面PCE 的距离为2.
(1)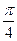 (2)
(2)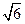
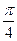 (2)
(2)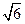
(1)设AD的中点为O,BC的中点为F,以O为原点,AD为x轴正半轴,AP为z轴正半轴,OF为y轴正半轴建立空间直角坐标系,连接OC,则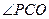 为PC与面AC所成的角,
为PC与面AC所成的角,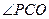 =
=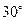 ,
,
设AD=2a,则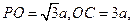 故
故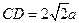 ,则
,则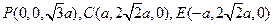 ,
,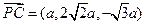 ,
,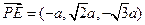 ,设平面PCE的一个法向量为
,设平面PCE的一个法向量为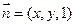 。
。
则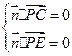 得
得 ,
,
又平面DCE的一个法向量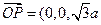 ),
),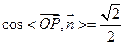 ,
,
故二面角P-CE-D为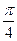 ………(8分)
………(8分)
(2)D(a,0,0),则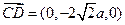 ,则点D到平面PCE的距离
,则点D到平面PCE的距离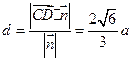
d=2,则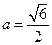 ,AD=
,AD=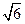 ………(12分)
………(12分)
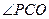 为PC与面AC所成的角,
为PC与面AC所成的角,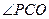 =
=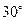 ,
,设AD=2a,则
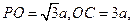 故
故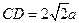 ,则
,则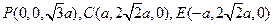 ,
,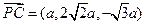 ,
,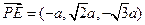 ,设平面PCE的一个法向量为
,设平面PCE的一个法向量为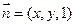 。
。则
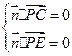 得
得 ,
,又平面DCE的一个法向量
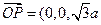 ),
),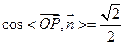 ,
,故二面角P-CE-D为
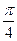 ………(8分)
………(8分)(2)D(a,0,0),则
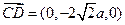 ,则点D到平面PCE的距离
,则点D到平面PCE的距离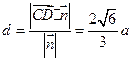
d=2,则
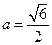 ,AD=
,AD=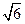 ………(12分)
………(12分)
练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
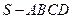 中,底面
中,底面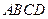 是菱形,
是菱形, ,
,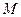 为
为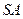 的中点,
的中点,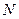 为
为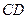 的中点.
的中点.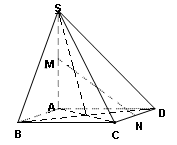
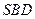
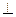 平面
平面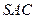 ;
;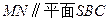 .
.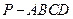 中,底面
中,底面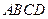 是直角梯形,
是直角梯形,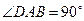 ,
,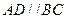 ,
,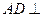 侧面
侧面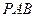 ,△
,△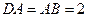 ,
, 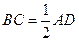 ,
,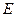 是线段
是线段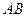 的中点.
的中点.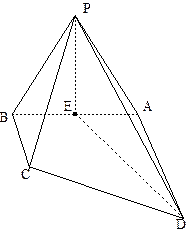
 ;
;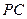 与平面
与平面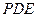 所成角的正弦值.
所成角的正弦值.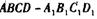 中,DA = DC
中,DA = DC =2,
=2,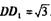 ’E是
’E是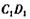 的中点,F是C/:的中点.
的中点,F是C/:的中点.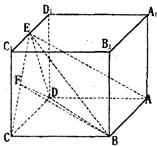
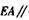 平面BDF
平面BDF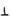 平面
平面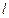
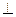 平面
平面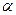 ,平面
,平面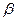 //直线
//直线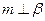 ,则
,则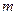 //
//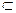
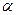 ,
,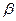 ,
,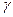 是三个不同平面,给出下列命题:
是三个不同平面,给出下列命题: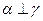 ,
,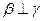 ,则
,则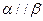 ;
;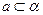 ,
,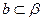 ,
,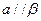 ,
,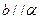 ,则
,则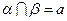 ,
,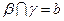 ,
,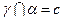 ,且
,且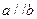 ,则
,则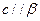 ;
;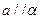 ,
,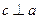 ,
,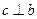 ,则
,则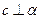 .
.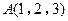 ,
,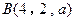 ,且
,且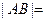
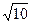 ,则
,则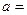 ( )
( )