题目内容
(本小题满分14分)
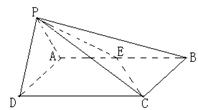
如图,四棱锥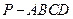 中,底面
中,底面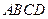 是直角梯形,
是直角梯形,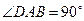 ,
,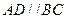 ,
,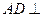 侧面
侧面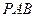 ,△
,△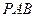 是等边三角形,
是等边三角形,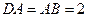 ,
, 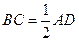 ,
,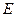 是线段
是线段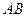 的中点.
的中点.
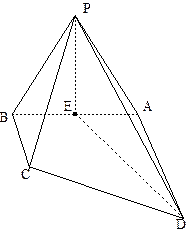
(Ⅰ)求证: ;
;
(Ⅱ)求四棱锥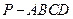 的体积;
的体积;
(Ⅲ)求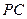 与平面
与平面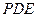 所成角的正弦值.
所成角的正弦值.
如图,四棱锥
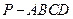 中,底面
中,底面 是直角梯形,
是直角梯形,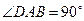 ,
,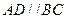 ,
,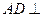 侧面
侧面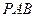 ,△
,△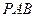 是等边三角形,
是等边三角形,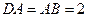 ,
, 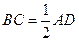 ,
,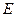 是线段
是线段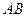 的中点.
的中点.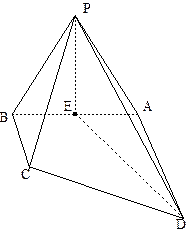
(Ⅰ)求证:
 ;
;(Ⅱ)求四棱锥
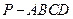 的体积;
的体积;(Ⅲ)求
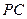 与平面
与平面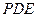 所成角的正弦值.
所成角的正弦值.(1)略(2) (3)
(3)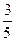
 (3)
(3)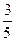
(Ⅰ)证明:因为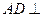 侧面
侧面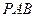 ,
,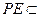 平面
平面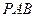 ,
,
所以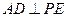 .……………………………………………………………2分
.……………………………………………………………2分
又因为△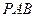 是等边三角形,
是等边三角形,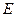 是线段
是线段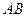 的中点,
的中点,
所以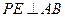 .
.
因为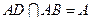 ,
,
所以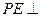 平面
平面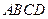 .…………………………………………………4分
.…………………………………………………4分
而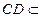 平面
平面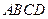 ,
,
所以 .……………………………………………………………5分
.……………………………………………………………5分
(Ⅱ)解:由(Ⅰ)知: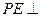 平面
平面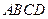 ,所以
,所以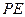 是四棱锥
是四棱锥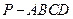 的高.
的高.
由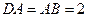 ,
,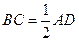 ,可得
,可得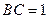 .
.
因为△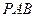 是等边三角形,
是等边三角形,
可求得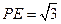 .
.
所以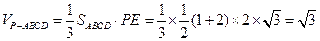 .………………9分
.………………9分
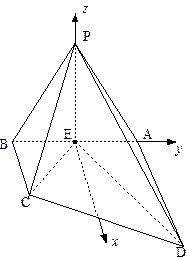
(Ⅲ)解:以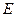 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系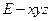 .
.
则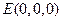 ,
,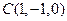 ,
,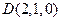 ,
, .
.
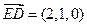 ,
,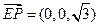 ,
,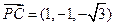 .
.
设 为平面
为平面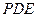 的法向量.
的法向量.
由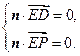 即
即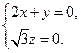
令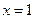 ,可得
,可得 .………………………12分
.………………………12分
设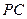 与平面
与平面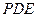 所成的角为
所成的角为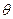 .
.
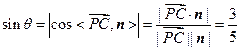 .
.
所以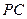 与平面
与平面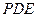 所成角的正弦值为
所成角的正弦值为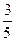 . …………………………………14分
. …………………………………14分
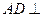 侧面
侧面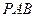 ,
,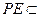 平面
平面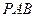 ,
, 所以
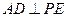 .……………………………………………………………2分
.……………………………………………………………2分又因为△
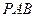 是等边三角形,
是等边三角形,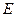 是线段
是线段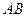 的中点,
的中点,所以
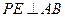 .
.因为
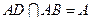 ,
,所以
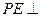 平面
平面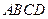 .…………………………………………………4分
.…………………………………………………4分而
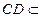 平面
平面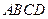 ,
,所以
 .……………………………………………………………5分
.……………………………………………………………5分(Ⅱ)解:由(Ⅰ)知:
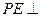 平面
平面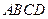 ,所以
,所以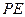 是四棱锥
是四棱锥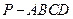 的高.
的高.由
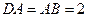 ,
,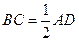 ,可得
,可得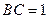 .
.因为△
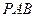 是等边三角形,
是等边三角形,可求得
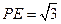 .
.所以
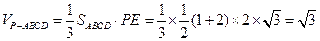 .………………9分
.………………9分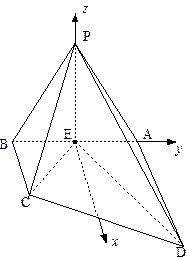
(Ⅲ)解:以
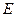 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系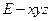 .
.则
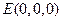 ,
,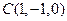 ,
,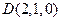 ,
, .
.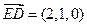 ,
,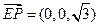 ,
,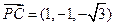 .
.设
 为平面
为平面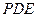 的法向量.
的法向量.由
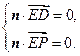 即
即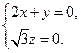
令
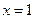 ,可得
,可得 .………………………12分
.………………………12分设
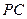 与平面
与平面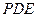 所成的角为
所成的角为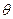 .
.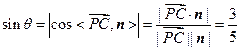 .
.所以
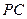 与平面
与平面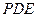 所成角的正弦值为
所成角的正弦值为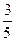 . …………………………………14分
. …………………………………14分
练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
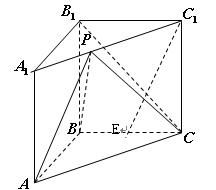
 ,E是AB的中点,PC与平面ABCD所成角为
,E是AB的中点,PC与平面ABCD所成角为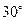 .
.
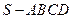 中,底面
中,底面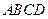 是正方形,其他四个侧面都是等边三角形,
是正方形,其他四个侧面都是等边三角形,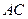 与
与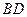 的交点为O.
的交点为O. 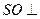 平面
平面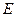 为侧棱
为侧棱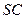 上一个动点. 试问对于
上一个动点. 试问对于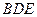 与平面
与平面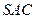 是否垂直?若垂直,请加以证明;若不垂直,请
是否垂直?若垂直,请加以证明;若不垂直,请 说明理由.
说明理由.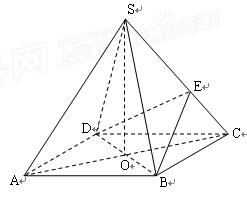
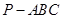 的四个顶点都在体积为
的四个顶点都在体积为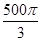 的球的表面上,平面
的球的表面上,平面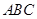 所在的小圆面积为
所在的小圆面积为 ,则该三棱锥的高的最大值是( )
,则该三棱锥的高的最大值是( )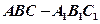 中,
中,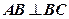 ,
,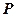 为
为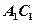 的中点,且
的中点,且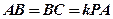 ,
,
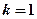 时,求证:
时,求证: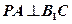 ;
;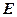 为
为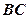 中点,当
中点,当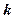 为何值时,异面直线
为何值时,异面直线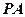
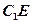 所成的角的正弦值为
所成的角的正弦值为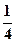 。
。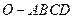 中,底面
中,底面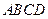 四边长为1的
四边长为1的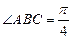 ,
,  ,
, 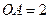 ,
,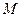 为
为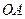 的中点.
的中点. ;
;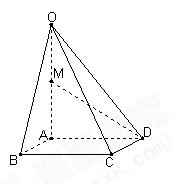
 BD B
BD B  为等边三角形
为等边三角形
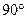 ,则称这对异面直线为“理想异面直线对”,在连结正方体各顶点的所有直线中,“理想异面直线对”的对数为
,则称这对异面直线为“理想异面直线对”,在连结正方体各顶点的所有直线中,“理想异面直线对”的对数为