题目内容
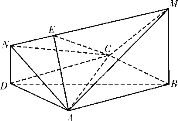
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是一个直角梯形,其中
是一个直角梯形,其中![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,点M和点N分别为
,点M和点N分别为![]() 和
和![]() 的中点.
的中点.
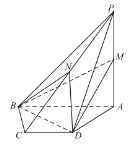
(1)证明:直线![]() 平面
平面![]() ;
;
(2)求直线![]() 和平面
和平面![]() 所成角的余弦值;
所成角的余弦值;
(3)求二面角![]() 的正弦值;
的正弦值;
(4)求点P到平面![]() 的距离;
的距离;
(5)设点N在平面![]() 内的射影为点H,求线段
内的射影为点H,求线段![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() ;(5)
;(5)![]()
【解析】
(1)以![]() 为原点,建立空间直角坐标系,利用向量法,证明
为原点,建立空间直角坐标系,利用向量法,证明![]() 与平面
与平面![]() 的法向量垂直,从而证明直线
的法向量垂直,从而证明直线![]() 平面
平面![]() .
.
(2)求出平面![]() 的法向量,利用向量法,求出直线
的法向量,利用向量法,求出直线![]() 和平面
和平面![]() 所成角的余弦值.
所成角的余弦值.
(3)求出平面![]() 的法向量和平面
的法向量和平面![]() 的法向量,利用向量法,求出二面角
的法向量,利用向量法,求出二面角![]() 的正弦值.
的正弦值.
(4)求出![]() 的坐标,再求出平面
的坐标,再求出平面![]() 的法向量
的法向量![]() ,利用向量法,求出点
,利用向量法,求出点![]() 到平面
到平面![]() 的距离;
的距离;
(5)设点![]() 在平面
在平面![]() 内的射影为点
内的射影为点![]() ,从而表示出
,从而表示出![]() 的坐标,求出
的坐标,求出![]() 到平面
到平面![]() 的距离
的距离![]() ,列出方程组,求出
,列出方程组,求出![]() 点坐标,从而求出
点坐标,从而求出![]() 的长度.
的长度.
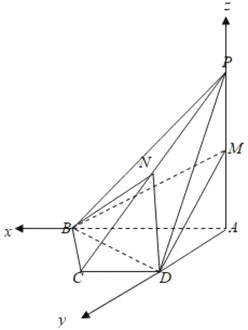
(1)四棱锥![]() ,底面
,底面![]() 是一个直角梯形,
是一个直角梯形,![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
所以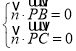 ,
,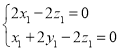 ,
,
取![]() ,则
,则![]() ,
,
所以![]() ,
,![]() 平面
平面![]() ,
,
所以直线![]() 平面
平面![]() .
.
(2)![]() ,
,![]() ,
,![]() ,
,![]()
设平面![]() 的法向量
的法向量![]() ,
,
则 ,即
,即 ,
,
取![]() ,则
,则![]() ,
,
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
则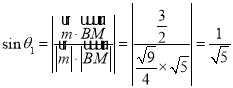 ,
,
所以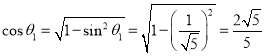 ,
,
所以直线![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
(3)设平面![]() 的法向量为
的法向量为![]() ,
,
则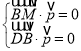 ,即
,即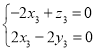 ,
,
取![]() ,得
,得![]() ,
,
平面![]() 的法向量
的法向量![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,
,
则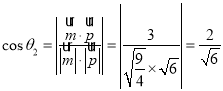 ,
,
所以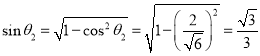 ,
,
所以二面角![]() 的正弦值为
的正弦值为![]() .
.
(4)![]() ,平面
,平面![]() 的法向量
的法向量![]() ,
,
所以点![]() 到平面
到平面![]() 的距离为
的距离为
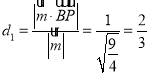 .
.
(5)设点![]() 在平面
在平面![]() 的射影为点
的射影为点![]() ,
,
则![]() ,
,
所以点![]() 到平面
到平面![]() 的距离为
的距离为 ,
,
根据 ,得
,得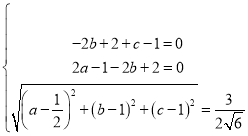
解得![]() ,
,![]() ,
,![]() ,或者
,或者![]() ,
,![]() ,
,![]() (舍)
(舍)
所以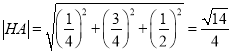 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某新上市的电子产品举行为期一个星期(7天)的促销活动,规定购买该电子产品可免费赠送礼品一份,随着促销活动的有效开展,第五天工作人员对前五天中参加活动的人数进行统计,![]() 表示第
表示第![]() 天参加该活动的人数,得到统计表格如下:
天参加该活动的人数,得到统计表格如下:
| 1 | 2 | 3 | 4 | 5 |
| 4 | 6 | 10 | 23 | 22 |
(1)若![]() 与
与![]() 具有线性相关关系,请根据上表提供的数据,用最小二乘法求出
具有线性相关关系,请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)预测该星期最后一天参加该活动的人数(按四舍五入取到整数).
参考公式: ,
,![]()