题目内容
20．已知an=cos$\frac{2nπ}{3}$，Sn是数列{an}的前n项和，则S2015=（ ）| A． | -2 | B． | -1 | C． | 0 | D． | 1 |
分析 由f（n）=cos$\frac{2nπ}{3}$是以T=3为周期的周期函数可得数列每相邻三项的和，则答案可求．
解答 解：an=cos$\frac{2nπ}{3}$
f（n）=cos$\frac{2nπ}{3}$是以T=3为周期的周期函数，
∴a1+a2+a3=-$\frac{1}{2}$-$\frac{1}{2}$+1=0，
…
a3k+1+a3k+2+a3k+3=0，
则S2015=a1+a2+a3+a4+…+a2015
=0×671+（-$\frac{1}{2}$-$\frac{1}{2}$）=-1．
故选B．
点评 本题考查了三角函数的周期性，考查了数列的求和，关键是对规律的发现，是中档题．
练习册系列答案
开心练习课课练与单元检测系列答案
开心试卷期末冲刺100分系列答案
双基同步导航训练系列答案
相关题目
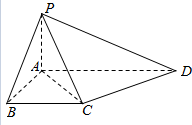如图，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是直角梯形，AD⊥AB，BC∥AD，AD=2AB=2BC=2．求证：PC⊥CD．
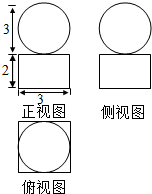设如图是某几何体的三视图，求该几何体的体积和表面积．