题目内容
10.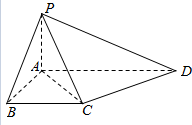 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,AD⊥AB,BC∥AD,AD=2AB=2BC=2.求证:PC⊥CD.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,AD⊥AB,BC∥AD,AD=2AB=2BC=2.求证:PC⊥CD.
分析 由题意可得:PA⊥CD,证明CD⊥AC,由线面垂直的判定定理可得CD⊥平面PAC,即可证明结论.
解答 证明:∵PA⊥平面ABCD,CD?平面ABCD,
∴PA⊥CD,
∵底面ABCD是直角梯形,AD⊥AB,BC∥AD,AD=2AB=2BC=2,
∴AC=$\sqrt{2}$,CD=$\sqrt{2}$,
∴AC2+CD2=AD2,
∴CD⊥AC,
∵PA∩AC=A,
∴CD⊥平面PAC,
∴PC⊥CD.
点评 本题主要考查线面垂直的判定定理,考查学生的空间想象能力与逻辑推理能力,解决此类问题的关键是熟练掌握有关的定理与几何体的结构特征,此题属于基础题,

练习册系列答案
相关题目
20.已知an=cos$\frac{2nπ}{3}$,Sn是数列{an}的前n项和,则S2015=( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |