Question

5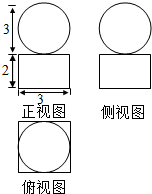．设如图是某几何体的三视图，求该几何体的体积和表面积．

Answer 1

分析 由已知中的三视图，可得该几何体是一个长方体和一个球形成的组合体，分别计算长方体和球的体积及面积，相加可得答案．

解答 解：由已知中的三视图，可得该几何体是一个长方体和一个球形成的组合体，
长方体的体积为3×3×2=18，球的体积为：$\frac{4}{3}•π•（\frac{3}{2}）^{3}$=$\frac{9}{2}π$，
故组合体的体积V=18+$\frac{9}{2}π$，
长方体的表面积为2（2×3+2×3+3×3）=42，球的表面积为：$4π•{（\frac{3}{2}）}^{2}$=9π，
故组合体的表面积S=42+9π．

点评 本题考查的知识点是由三视图求体积和表面积，根据三视图判断出几何体的形状是解答的关键．