题目内容
15.设曲线y=xn+1(n∈N*)在点(1,1)处的切线与y轴的交点的纵坐标为yn,令bn=2yn,b1•b2•…b2010的值为22010•2010!.分析 先求出其导函数,把x=1代入,求出切线的斜率,进而得到切线方程,找到切线与y轴的交点的纵坐标的表达式,即可求出结论.
解答 解:因为y=xn+1,
故y′=(n+1)xn,
所以x=1时,y′=n+1,
则直线方程为y-1=(n+1)(x-1),
令x=0,则y=1-(n+1)=-n,
故切线与y轴的交点为( 0,-n),
即有bn=2yn=-2n,
则b1•b2•…b2010=(-2)×(-4)×…×(-4020)
=22010•2010!.
故答案为:22010•2010!.
点评 当题目中遇到求曲线C在点A(m,n)的切线方程时,其处理步骤为:①判断A点是否在C上②求出C对应函数的导函数③求出过A点的切线的斜率④代入点斜式方程,求出直线的方程.同时考查运算能力,属于中档题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
6.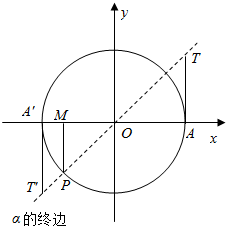 如图所示,P是角α得终边与单位圆的交点,PM⊥x轴于M,AT和A′T′均是单位圆的切线,则角α的( )
如图所示,P是角α得终边与单位圆的交点,PM⊥x轴于M,AT和A′T′均是单位圆的切线,则角α的( )
 如图所示,P是角α得终边与单位圆的交点,PM⊥x轴于M,AT和A′T′均是单位圆的切线,则角α的( )
如图所示,P是角α得终边与单位圆的交点,PM⊥x轴于M,AT和A′T′均是单位圆的切线,则角α的( )| A. | 正弦值是PM,正切线是A′T′ | B. | 正弦值是MP,正切线是A′T′ | ||
| C. | 正弦值是MP,正切线是AT | D. | 正弦值是PM,正切线是AT |
3.下列直线是函数y=log2x和y=log${\;}_{\frac{1}{2}}$4x的图象对称轴的为( )
| A. | x=1 | B. | x=-1 | C. | y=1 | D. | y=-1 |
20.已知an=cos$\frac{2nπ}{3}$,Sn是数列{an}的前n项和,则S2015=( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
7.不等式$\frac{1}{1+lgx}$+$\frac{1}{1-lgx}$>2的解集为( )
| A. | ($\frac{1}{10}$,1)∪(1,10) | B. | ($\frac{1}{10}$,1)∪(2,10) | C. | ($\frac{1}{10}$,10) | D. | (1,+∞) |
5.一个物体的运动方程为s=1-t+t2,其中s的单位是m,t的单位是s,那么物体在最初3s内的平均速度是( )
| A. | 7m/s | B. | 6m/s | C. | 2m/s | D. | 1m/s |