Question

16．已知点P（0，-1），Q（0，1），若直线 l：y=mx-2 上至少存在三个点 M，使得△PQM 为直角三角形，则实数 m 的取值范围是m≤-$\sqrt{3}$或m≥$\sqrt{3}$．

Answer 1

分析 由直径对的圆周角是直角，知直线和以PQ为直径的圆有公共点即可，由此能求出实数m的取值范围，

解答 解：若直线 l：y=mx-2 上至少存在三个点 M，使得△PQM 为直角三角形，
则m≠0，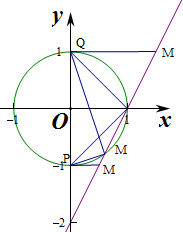
若∠PQM=90°，则此时存在一个M，
若∠MQP=90°，则此时存在一个M，
若∠QMP=90°，由直径对的圆周角是直角，知直线和以PQ为直径的圆有公共点即可，
以PQ为直径的圆的方程为x²+y²=1，
则满足圆心到直线的距离d=$\frac{|2|}{\sqrt{{m}^{2}+1}}≤1$，
即m²+1≥4
则m²≥3，解得m≤-$\sqrt{3}$或m≥$\sqrt{3}$，
故答案为：m≤-$\sqrt{3}$或m≥$\sqrt{3}$．

点评 本题考查直线与圆的位置关系等基础知识，意在考查运用方程思想求解能力，考查数形结合思想的灵活运用．