题目内容
1.已知函数 f(x)=ax-lnx,g(x)=eax+2x,其中 a∈R.(Ⅰ)当 a=2 时,求函数 f(x) 的极值;
(Ⅱ)若存在区间 D⊆(0,+∞),使得 f(x)与g(x)在区间D上具有相同的单调性,求a的取值范围.
分析 (Ⅰ)当a=2时,f′(x)=2-$\frac{1}{x}$,通过f′(x)的符号可判断f(x)在相应区间上的单调性,从而可求得f(x)的极值;
(Ⅱ)可求得f′(x)=a-$\frac{1}{x}$,g′(x)=aeax+2,对a分a>0,a=0与a<0讨论,通过f′(x)的符号可判断f(x)在相应区间上的单调性,可求得a的取值范围.
解答 解:(Ⅰ)当a=2时,f′(x)=2-$\frac{1}{x}$,
故当x∈(0,$\frac{1}{2}$)时,f(x)单调递减;当x∈($\frac{1}{2}$,+∞)时,f(x)单调递增;
所以,f(x)在x=$\frac{1}{2}$处取得极小值f($\frac{1}{2}$)=1+ln2,无极大值; …(5分)
(Ⅱ)f′(x)=a-$\frac{1}{x}$,g′(x)=aeax+2,
当a>0时,g′(x)>0,即g(x)在R上单调递增,而f(x)在($\frac{1}{a}$,+∞)上单调递增,
故必存在D⊆(0,+∞),使得f(x)与g(x)在D上单调递增;
当a=0时,f′(x)=-$\frac{1}{x}$<0,故f(x)在(0,+∞)上单调递减,而g(x)在(0,+∞)上单调递增,
故不存在满足条件的区间D;
当a<0时,f′(x)=a-$\frac{1}{x}$<0,即f(x)在(0,+∞)上单调递减,而g(x)在(-∞,$\frac{1}{a}ln(-\frac{2}{a})$)上单调递减,($\frac{1}{a}ln(-\frac{2}{a})$,+∞)上单调递增,若存在存在D⊆(0,+∞),使得f(x)与g(x)在D上上单调性相同,
则有$\frac{1}{a}ln(-\frac{2}{a})$>0,解得a<-2;
综上,a>0或a<-2.…(12分)
点评 本题考查函数在某点取得极值的条件,考查利用导数研究函数的单调性,突出考查分类讨论思想与方程思想,属于难题.

| 志愿 | 第一志愿 | 第二志愿 | 第三志愿 |
| 学校 | 1 | 2 | 3 |
| 专业 | 第1专业 | 第1专业 | 第1专业 |
| 第2专业 | 第2专业 | 第2专业 |
| A. | 3-2$\sqrt{3}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{1}{4}$ |
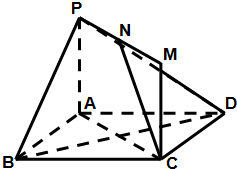 如图,矩形ACMP和菱形ABCD所在的平面互相垂直,点N为PM的中点,
如图,矩形ACMP和菱形ABCD所在的平面互相垂直,点N为PM的中点,