题目内容
4.在△ABC中,若$\frac{{a}^{2}}{{b}^{2}}$=$\frac{sinAcosB}{cosAsinB}$,判断△ABC的形状.分析 由正弦定理结合三角形内角的范围可求得sin2A=sin2B,根据和差化积公式整理求得cos(A+B)=0或sin(A-B)=0,推断出A+B=$\frac{π}{2}$或A=B,则三角形形状可判断出.
解答 解:∵由正弦定理可得:a=2RsinA,b=2RsinB,
∴$\frac{{a}^{2}}{{b}^{2}}$=$\frac{4{R}^{2}si{n}^{2}A}{4{R}^{2}si{n}^{2}B}$=$\frac{si{n}^{2}A}{si{n}^{2}B}$=$\frac{sinAcosB}{cosAsinB}$,
∵0<A<π,0<B<π,即sinA>0,sinB>0,
∴可得:$\frac{sinA}{sinB}=\frac{cosB}{cosA}$,解得sin2A=sin2B,
∴sin2A-sin2B=cos(A+B)sin(A-B)=0,
∴cos(A+B)=0或sin(A-B)=0,
∴A+B=$\frac{π}{2}$或A=B,
∴三角形为直角三角形或等腰三角形.
点评 本题主要考查了三角形的形状判断.需要挖掘题设信息,借助三角函数的基本公式和基本性质找到边与边或角与角之间的关系,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下面是高考第一批录取的一份志愿表:
现有4所重点院校,每所院校有3个专业是你较为满意的选择,如果从中任选3所随意填报,表格填满且规定学校没有重复,同一学校的专业也没有重复的话,不同的填写方法的种数是多少?
| 志愿 | 第一志愿 | 第二志愿 | 第三志愿 |
| 学校 | 1 | 2 | 3 |
| 专业 | 第1专业 | 第1专业 | 第1专业 |
| 第2专业 | 第2专业 | 第2专业 |
19.曲线y=ex,直线x=0,x=$\frac{1}{2}$与x轴围成的平面图形绕x轴旋转一周得到旋转体的体积是( )
| A. | $\frac{(e-1)π}{2}$ | B. | $\frac{(e-1){π}}{3}$ | C. | $\frac{(e-1)π}{4}$ | D. | $\frac{(e-1)π}{5}$ |
 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),离心率为e,过椭圆焦点F的直线l交椭圆于A、B两点,倾斜角为θ.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),离心率为e,过椭圆焦点F的直线l交椭圆于A、B两点,倾斜角为θ.



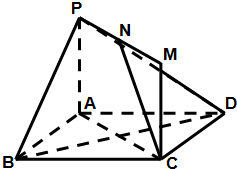 如图,矩形ACMP和菱形ABCD所在的平面互相垂直,点N为PM的中点,
如图,矩形ACMP和菱形ABCD所在的平面互相垂直,点N为PM的中点,