题目内容
若双曲线的两条渐近线的夹角为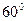
，则该双曲线的离心率为（ ）
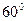，则该双曲线的离心率为（ ）| A．2 | B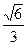． | C．2或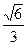 | D．2或 |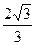
D
首先根据题意要对焦点位置进行分类讨论：第一种就是焦点在x轴上，这时
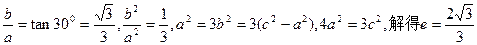；第二种就是焦点在y轴上，这时
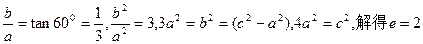,故答案选D。
练习册系列答案
相关题目
D
首先根据题意要对焦点位置进行分类讨论：第一种就是焦点在x轴上，这时
；第二种就是焦点在y轴上，这时,故答案选D。题目内容
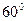，则该双曲线的离心率为（ ）| A．2 | B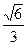． | C．2或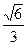 | D．2或 |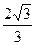
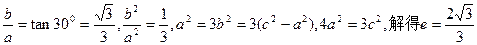；第二种就是焦点在y轴上，这时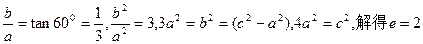,故答案选D。
·
=1，
<S<2,求向量
c,若以O为中心，F为焦点的椭圆经过点Q，当|
|取得最小值时，求此椭圆的方程.
，焦点F2到渐近线的距离为
，两条准线之间的距离为1。 （I）求此双曲线的方程； （II）过双曲线焦点F1的直线与双曲线的两支分别相交于A、B两点，过焦点F2且与AB平行的直线与双曲线分别相交于C、D两点，若A、B、C、D这四点依次构成平行四边形ABCD，且
，求直线AB的方程。
的两个顶点
的坐标分别为
，
，平面内两点
同时满足下列条件：
；②
；③
∥
的轨迹方程；
的直线
与（1）中轨迹交于
两点，求
的取值范围
上
的值
和椭圆
有相同的焦点
和
，两曲线在第一象限内的交点为
，椭圆
轴负半轴交于点
，且
三点共线，
分有向线段
的比为
，又直线
与双曲线
，若
．
||
|+ 
=0，求动点P（x，y）的轨迹方程.
，求直线l的方程；
上点
到定点
和焦点
的距离之和的最小值为
，求此抛物线的方程．