题目内容
(本小题满分12分)已知四棱锥P—ABCD,
底面ABCD是菱形,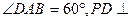 平面ABCD,PD=AD,点E为AB中点,点F为PD中点。 (1)证明平面PED⊥平面PAB; (2)求二面角P—AB—F的平面角的余弦值。
平面ABCD,PD=AD,点E为AB中点,点F为PD中点。 (1)证明平面PED⊥平面PAB; (2)求二面角P—AB—F的平面角的余弦值。
底面ABCD是菱形,
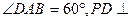 平面ABCD,PD=AD,点E为AB中点,点F为PD中点。 (1)证明平面PED⊥平面PAB; (2)求二面角P—AB—F的平面角的余弦值。
平面ABCD,PD=AD,点E为AB中点,点F为PD中点。 (1)证明平面PED⊥平面PAB; (2)求二面角P—AB—F的平面角的余弦值。(Ⅰ) (Ⅱ) (Ⅲ)
解法一(1)证明:连接BD.

 为等边三角形.
为等边三角形.
 是AB中点,
是AB中点,
 面ABCD,AB
面ABCD,AB 面ABCD,
面ABCD,
 面PED,PD
面PED,PD 面PED,
面PED,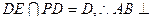 面PED。
面PED。
 面PAB,
面PAB, 面PAB.
面PAB.
(2)解: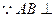 平面PED,PE
平面PED,PE 面PED,
面PED,
 连接EF,
连接EF, PED,
PED,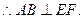
 为二面角P—AB—F的平面角.
为二面角P—AB—F的平面角.
设AD=2,那么PF=FD=1,DE= .
.
在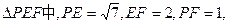

即二面角P—AB—F的平面角的余弦值为
解法二:如图连结DE,则DE⊥DC,则可以以D为坐标原点,DE,DC,DP所在直线分别为x、y,z轴建立空间直角坐标系,设菱形ABCD的长为a,则: ,
,
则P(0,0, ),F(0,0,
),F(0,0, ),A(
),A( ),B(
),B( ),
), (
( ),
),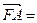 (
( ),
), (0,
(0, ,0)
,0)
设平面 的法向量为
的法向量为 ,平面
,平面 的法向量为
的法向量为
 ,令
,令 ,可得
,可得
 ,令
,令 ,可得
,可得
 显然,二面角P-AB-F的平面角是锐角与
显然,二面角P-AB-F的平面角是锐角与 大小相等,
大小相等,
即二面角P-AB-F的平面角的余弦值为

 为等边三角形.
为等边三角形. 是AB中点,
是AB中点,
 面ABCD,AB
面ABCD,AB 面ABCD,
面ABCD,
 面PED,PD
面PED,PD 面PED,
面PED,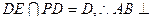 面PED。
面PED。 面PAB,
面PAB, 面PAB.
面PAB. (2)解:
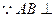 平面PED,PE
平面PED,PE 面PED,
面PED,
 连接EF,
连接EF, PED,
PED,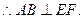
 为二面角P—AB—F的平面角.
为二面角P—AB—F的平面角. 设AD=2,那么PF=FD=1,DE=
 .
. 在
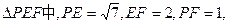

即二面角P—AB—F的平面角的余弦值为

解法二:如图连结DE,则DE⊥DC,则可以以D为坐标原点,DE,DC,DP所在直线分别为x、y,z轴建立空间直角坐标系,设菱形ABCD的长为a,则:
 ,
,则P(0,0,
 ),F(0,0,
),F(0,0, ),A(
),A( ),B(
),B( ),
), (
( ),
),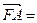 (
( ),
), (0,
(0, ,0)
,0)设平面
 的法向量为
的法向量为 ,平面
,平面 的法向量为
的法向量为
 ,令
,令 ,可得
,可得
 ,令
,令 ,可得
,可得
 显然,二面角P-AB-F的平面角是锐角与
显然,二面角P-AB-F的平面角是锐角与 大小相等,
大小相等,即二面角P-AB-F的平面角的余弦值为


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的底面是边长为1的正方形,
的底面是边长为1的正方形, 底面
底面 ,
, 。
。
 ;
;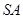 的中点为
的中点为 ,求异面直线
,求异面直线 与
与 所成角的大小;
所成角的大小; 底面ABCD,当
底面ABCD,当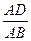 的值等于多少时,能使PB
的值等于多少时,能使PB
 中,面
中,面 与面
与面 成
成 的二面角,顶点
的二面角,顶点 在面
在面 是
是 的垂心,
的垂心, 是
是 的重心,若
的重心,若 ,
, ,则
,则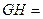 .
. 
 的斜线
的斜线 交
交 ,过定点
,过定点 的动直线
的动直线 与
与 ,则动点
,则动点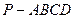 中,
中, 平面
平面 ,底面
,底面 .
.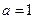 时,求证:
时,求证: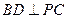 ;
; 边上有且只有一个点
边上有且只有一个点 ,使得
,使得 ,求此时二面角
,求此时二面角 的余弦值.
的余弦值.
 ,甲、乙两地均在本初子午线(
,甲、乙两地均在本初子午线( 经线上),且甲地位于北纬
经线上),且甲地位于北纬 ,乙地位于南纬
,乙地位于南纬 ,则甲、乙两地的球面距离为
,则甲、乙两地的球面距离为