题目内容
四面体 中,面
中,面 与面
与面 成
成 的二面角,顶点
的二面角,顶点 在面
在面 上的射影
上的射影 是
是 的垂心,
的垂心, 是
是 的重心,若
的重心,若 ,
, ,则
,则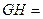 .
.

 中,面
中,面 与面
与面 成
成 的二面角,顶点
的二面角,顶点 在面
在面 上的射影
上的射影 是
是 的垂心,
的垂心, 是
是 的重心,若
的重心,若 ,
, ,则
,则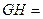 .
. 
: .
.
 .
.:设面 交
交 于
于 ,则因
,则因 ,故
,故 在
在 上,且
上,且 ,
,
 ,于是
,于是 ,
, ,
, ,在三角形
,在三角形 中,由余弦定理得
中,由余弦定理得
 交
交 于
于 ,则因
,则因 ,故
,故 在
在 上,且
上,且 ,
, ,于是
,于是 ,
, ,
, ,在三角形
,在三角形 中,由余弦定理得
中,由余弦定理得

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
题目内容
 中,面
中,面 与面
与面 成
成 的二面角,顶点
的二面角,顶点 在面
在面 上的射影
上的射影 是
是 的垂心,
的垂心, 是
是 的重心,若
的重心,若 ,
, ,则
,则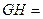 .
. 
 .
. 交
交 于
于 ,则因
,则因 ,故
,故 在
在 上,且
上,且 ,
, ,于是
,于是 ,
, ,
, ,在三角形
,在三角形 中,由余弦定理得
中,由余弦定理得

 小学课时特训系列答案
小学课时特训系列答案