题目内容
(本小题满分12分)
在四棱锥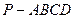 中,
中, 平面
平面 ,底面
,底面 为矩形,
为矩形, .
.
(I)当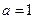 时,求证:
时,求证: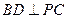 ;
;
(II)若 边上有且只有一个点
边上有且只有一个点 ,使得
,使得 ,求此时二面角
,求此时二面角 的余弦值.
的余弦值.
在四棱锥
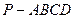 中,
中, 平面
平面 ,底面
,底面 为矩形,
为矩形, .
.(I)当
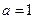 时,求证:
时,求证: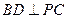 ;
;(II)若
 边上有且只有一个点
边上有且只有一个点 ,使得
,使得 ,求此时二面角
,求此时二面角 的余弦值.
的余弦值.
(I)略(II)

(I)当 时,底面
时,底面 为正方形,
为正方形,

又因为 ,
, 面
面 …………………………2分
…………………………2分
又 面
面
 …………………………3分
…………………………3分
(II)因为 两两垂直,分别以它们所在直线为
两两垂直,分别以它们所在直线为 轴、
轴、 轴、
轴、 轴建立坐标系,如图所示,令
轴建立坐标系,如图所示,令 ,可得
,可得

则 …………………4分
…………………4分
设 ,则
,则
要使 ,只要
,只要
即 ………6分
………6分
由
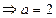 ,此时
,此时 。
。
所以 边上有且只有一个点
边上有且只有一个点 ,使得
,使得 时,
时,
 为
为 的中点,且
的中点,且 …………………………8分
…………………………8分
设面 的法向量
的法向量
则 即
即 解得
解得 …………………………10分
…………………………10分
取平面 的法向量
的法向量
则 的大小与二面角
的大小与二面角 的大小相等
的大小相等
所以
因此二面角 的余弦值为
的余弦值为 …………………………12分
…………………………12分
 时,底面
时,底面 为正方形,
为正方形,

又因为
 ,
, 面
面 …………………………2分
…………………………2分又
 面
面
 …………………………3分
…………………………3分(II)因为
 两两垂直,分别以它们所在直线为
两两垂直,分别以它们所在直线为 轴、
轴、 轴、
轴、 轴建立坐标系,如图所示,令
轴建立坐标系,如图所示,令 ,可得
,可得

则
 …………………4分
…………………4分设
 ,则
,则
要使
 ,只要
,只要
即
 ………6分
………6分由

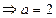 ,此时
,此时 。
。所以
 边上有且只有一个点
边上有且只有一个点 ,使得
,使得 时,
时, 为
为 的中点,且
的中点,且 …………………………8分
…………………………8分设面
 的法向量
的法向量
则
 即
即 解得
解得 …………………………10分
…………………………10分取平面
 的法向量
的法向量
则
 的大小与二面角
的大小与二面角 的大小相等
的大小相等所以

因此二面角
 的余弦值为
的余弦值为 …………………………12分
…………………………12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,D∈
,D∈ ,
, ,E为BC的中点,AC⊥BD,BD=8.
,E为BC的中点,AC⊥BD,BD=8.
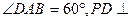 平面ABCD,PD=AD,点E为AB中点,点F为PD中点。 (1)证明平面PED⊥平面PAB; (2)求二面角P—AB—F的平面角的余弦值。
平面ABCD,PD=AD,点E为AB中点,点F为PD中点。 (1)证明平面PED⊥平面PAB; (2)求二面角P—AB—F的平面角的余弦值。 ,D是线段A1B1的中点.
,D是线段A1B1的中点. 
 ⊥平面A1B1BA;
⊥平面A1B1BA; ;
;

 ,
, ,M、N分别为棱PA 、PD的中点,问在底面正方形的对角线AC上是否存在一点F,使EF//平面LMN. 若存在,请具体求出CF的长度;若不存在,请说明理由.
,M、N分别为棱PA 、PD的中点,问在底面正方形的对角线AC上是否存在一点F,使EF//平面LMN. 若存在,请具体求出CF的长度;若不存在,请说明理由.
 中,棱长
中,棱长 .
. 为棱
为棱 的中点,求证:
的中点,求证: ;
; 的大小;
的大小; 到平面
到平面 的距离.
的距离. 为平面,
为平面, 为直线,则
为直线,则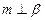 的一个充分条件是
的一个充分条件是




 中,
中,
 的中点,给出如下三个结论:①
的中点,给出如下三个结论:①
 ③平面
③平面 ,其中正确结论为 (填序号)
,其中正确结论为 (填序号)