题目内容
四棱锥P-ABCD的底面是矩形,侧面PAD是正三角形,且侧面PAD 底面ABCD,当
底面ABCD,当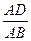 的值等于多少时,能使PB
的值等于多少时,能使PB AC?并给出证明.
AC?并给出证明.

 底面ABCD,当
底面ABCD,当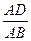 的值等于多少时,能使PB
的值等于多少时,能使PB AC?并给出证明.
AC?并给出证明.
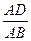 =
= 时,能使PB
时,能使PB AC
AC当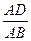 =
= 时,能使PB
时,能使PB AC
AC
证明:取AD中点F,连接PF,
 PF
PF AD,面PAD
AD,面PAD 面ABCD,
面ABCD,
 PF
PF 面ABCD,
面ABCD,
连结BF,交AC于O,则根据题意,当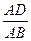 =
= 时,有
时,有
AC= AB,AF=
AB,AF= AB,A
AB,A O=
O= AB,FO=
AB,FO= AB.
AB.
∴AF2=AO2+FO2,即FB AC,
AC,
由三垂线定理可证得PB AC.
AC.
∴当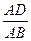 =
= 时,能使PB
时,能使PB AC.
AC.
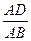 =
= 时,能使PB
时,能使PB AC
AC证明:取AD中点F,连接PF,
 PF
PF AD,面PAD
AD,面PAD 面ABCD,
面ABCD, PF
PF 面ABCD,
面ABCD,连结BF,交AC于O,则根据题意,当
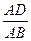 =
= 时,有
时,有AC=
 AB,AF=
AB,AF= AB,A
AB,A O=
O= AB,FO=
AB,FO= AB.
AB.∴AF2=AO2+FO2,即FB
 AC,
AC,由三垂线定理可证得PB
 AC.
AC.∴当
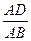 =
= 时,能使PB
时,能使PB AC.
AC.
练习册系列答案
相关题目

 (Ⅰ)求证:MN⊥平面A1BC;
(Ⅰ)求证:MN⊥平面A1BC;
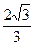 为半径作一个球,则球面与正方体的表面相交所得到的曲线的长等于 。
为半径作一个球,则球面与正方体的表面相交所得到的曲线的长等于 。 则此球的表面积为
则此球的表面积为 .
. ,D∈
,D∈ ,
, ,E为BC的中点,AC⊥BD,BD=8.
,E为BC的中点,AC⊥BD,BD=8.
 中,
中, 上是否存在一个点P,使得直线
上是否存在一个点P,使得直线 与平面
与平面 所成角的正切值为
所成角的正切值为
 ;(Ⅱ)若P是侧棱
;(Ⅱ)若P是侧棱 上是否存在一个定点
上是否存在一个定点 ,使得
,使得 在平面
在平面 上的射影垂直于
上的射影垂直于 为原正方体的顶点,
为原正方体的顶点, 为原正方体一条棱的中点。在原来的正方体中,
为原正方体一条棱的中点。在原来的正方体中, 与
与 所成角的余弦值为 ( )
所成角的余弦值为 ( )




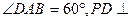 平面ABCD,PD=AD,点E为AB中点,点F为PD中点。 (1)证明平面PED⊥平面PAB; (2)求二面角P—AB—F的平面角的余弦值。
平面ABCD,PD=AD,点E为AB中点,点F为PD中点。 (1)证明平面PED⊥平面PAB; (2)求二面角P—AB—F的平面角的余弦值。

 ,
, ,M、N分别为棱PA 、PD的中点,问在底面正方形的对角线AC上是否存在一点F,使EF//平面LMN. 若存在,请具体求出CF的长度;若不存在,请说明理由.
,M、N分别为棱PA 、PD的中点,问在底面正方形的对角线AC上是否存在一点F,使EF//平面LMN. 若存在,请具体求出CF的长度;若不存在,请说明理由.