题目内容

12．设某几何体的三视图如图所示，则该几何体的体积为24π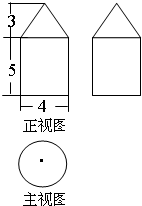

分析 由三视图可知，几何体是底部是一底面半径为2，高为5的圆柱，上部为底面半径为2，高为3的圆锥，分别计算两部分的体积，即可．

解答 解：由三视图可知，几何体是底部是一底面半径为2，高为5的圆柱，上部为底面半径为2，高为3的圆锥，
圆柱的体积为V1=4π×5=20π，圆锥的体积为：V2=$\frac{1}{3}×{2}^{2}π×3=4π$
故几何体的体积为V=V1+V2=24π．
故答案为：24π．

点评 本题考查三视图求几何体的体积，考查计算能力，空间想象能力，三视图复原几何体是解题的关键．

练习册系列答案
相关题目
2．已知函数f（x）=$\frac{x}{x+1}$（x≠-1）．
（1）求f（x）的单调区间；
（2）若a＞b＞0，且c=$\frac{1}{b（a-b）}$，求证：f（a）+f（c）$＞\frac{3}{4}$．
3．研究直线y=mx+1（x∈R）在矩阵$[\begin{array}{cc}1&0\\ 0&-1\end{array}\right.]$对应的变换作用下得到的图形．
20．已知复数（1-i2015）•Z=i2014，则Z的共轭复数在复平面中对应的点在（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
7．在△ABC中，内角A、B、C的对边分别为a、b、c，已知a-b=2，c=4，sinA=2sinB．
（1）求△ABC的面积；
（2）求tan（A-B）．
17．已知矩阵A=$[\begin{array}{l}{1}&{2}\\{-1}&{4}\end{array}]$，向量$\overrightarrow{a}$=$[\begin{array}{l}{7}\\{4}\end{array}]$．
（1）求A的特征值和对应的特征向量；
（2）计算A5α的值．
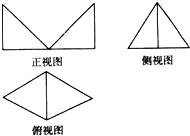4．某几何体的三视图如图，其侧视图是一个边长为1的等边三角形，俯视图是由两个等边三角形拼成，则该几何体的体积为$\frac{1}{4}$．
1．一颗骰子A，两面上写的是1，两面上写的是3，一面是4，一面是5；另一颗骰子B，一面是1，一面是2，三面是3，一面是5．如果两个骰子都放在一个袋中，从里面取出一颗骰子并且掷到桌上，问得到1，2，3，4，5的概率分别是$\frac{1}{4}$，$\frac{1}{12}$，$\frac{5}{12}$，$\frac{1}{12}$．
2．设x，y满足约束条件$\left\{\begin{array}{l}{y≤x}\\{x+y≥2}\\{x≤2}\end{array}\right.$，则z=2x+y+1的最大值为（　　）
A．5B．6C．7D．8

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网