题目内容
7.在△ABC中,内角A、B、C的对边分别为a、b、c,已知a-b=2,c=4,sinA=2sinB.(1)求△ABC的面积;
(2)求tan(A-B).
分析 (1)已知等式sinA=2sinB利用正弦定理化简得到a=2b,与a-b=2联立求出a与b的值,再由余弦定理求出cosB的值,进而求出sinB的值,利用三角形面积公式即可求出三角形ABC面积;
(2)由cosA的值求出sinA的值,进而求出sinB的值,利用同角三角函数间的基本关系求出cosB的值,确定出tanA与tanB的值,原式利用两角和与差的正切函数公式化简,将各自的值代入计算即可求出值.
解答 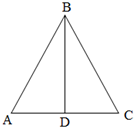 解:(1)由sinA=2sinB,根据正弦定理得a=2b,
解:(1)由sinA=2sinB,根据正弦定理得a=2b,
又∵a-b=2,
∴a=4,b=2,
由余弦定理得cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{16+16-4}{2×4×4}$=$\frac{7}{8}$>0,sinB=$\sqrt{1-co{s}^{2}B}$=$\frac{\sqrt{15}}{8}$,
∴S△ABC=$\frac{1}{2}$acsinB=$\sqrt{15}$;
(2)∵cosA=$\frac{1}{4}$>0,∴sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{\sqrt{15}}{4}$,
∴sinB=$\frac{1}{2}$sinA=$\frac{\sqrt{15}}{8}$,
∵b<c,∴B<C,
∴0<B<$\frac{π}{2}$,
∴cosB=$\sqrt{1-si{n}^{2}B}$=$\frac{7}{8}$,
∴tanA=$\frac{sinA}{cosA}$=$\sqrt{15}$,tanB=$\frac{sinB}{cosB}$=$\frac{\sqrt{15}}{7}$,
∴tan(A-B)=$\frac{tanA-tanB}{1+tanAtanB}$=$\frac{\sqrt{15}-\frac{\sqrt{15}}{7}}{1+\sqrt{15}×\frac{\sqrt{15}}{7}}$=$\frac{3\sqrt{15}}{11}$.
点评 此题考查了正弦、余弦定理,三角形面积公式,以及同角三角函数间的基本关系,熟练掌握定理及公式是解本题的关键.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案| A. | (-3,-2] | B. | [-2,-1) | C. | [-1,2) | D. | [2,3) |
| A. | 24 | B. | 25 | C. | 26 | D. | 27 |
| A. | (-∞,0)∪($\frac{1}{2}$,+∞) | B. | [0,$\frac{1}{2}$] | C. | (0,$\frac{1}{2}$ ) | D. | (-∞,0]∪[$\frac{1}{2}$,+∞) |
| A. | 3 | B. | 0 | C. | -4 | D. | -5 |