题目内容
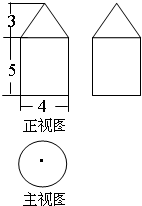
4．
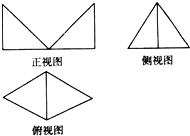某几何体的三视图如图，其侧视图是一个边长为1的等边三角形，俯视图是由两个等边三角形拼成，则该几何体的体积为$\frac{1}{4}$．
分析 根据几何体的三视图，得出该几何体是两个形状相同的直三棱锥，根据图中数据求出它的体积即可．
解答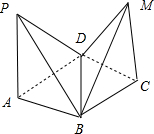 
解：根据几何体的三视图，得；
该几何体是两个形状相同的直三棱锥，
且三棱锥的底面是边长为1的等边三角形，高为$\frac{\sqrt{3}}{2}$；
如图所示，
所以该几何体的体积为
V=2×$\frac{1}{3}$×$\frac{1}{2}$×12×sin60°×（1×sin60°）=$\frac{1}{4}$．
故答案为：$\frac{1}{4}$．
点评 本题考查了空间几何体的三视图的应用问题，解题的关键是由三视图得出几何体的结构特征，是基础题目．
练习册系列答案
习题精选系列答案
相关题目
14．已知a、b、c均大于1，且logca•logcb=$\frac{1}{4}$，则下列不等式一定成立的是（ ）
| A． | ac≥b | B． | ab≥c | C． | bc≥a | D． | ab≤c |
19．函数f（x）=ln（x-2x2）的定义域为（ ）
| A． | （-∞，0）∪（$\frac{1}{2}$，+∞） | B． | [0，$\frac{1}{2}$] | C． | （0，$\frac{1}{2}$ ） | D． | （-∞，0]∪[$\frac{1}{2}$，+∞） |
9．集合A={-1，0，1，2，3}，B={-2，-1，0，1}，则图中阴影部分表示的集合为（ ）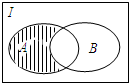
| A． | {-1，0，1} | B． | {2，3} | C． | {-2，2，3} | D． | {-1，0，1，2，3} |
16．执行如图中的程序，如果输出的结果是-4，那么输入的x只可能是（ ）
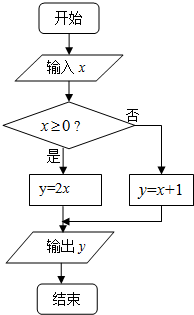
| A． | 3 | B． | 0 | C． | -4 | D． | -5 |
13．已知正四棱柱底面边长为1高为2，俯视图是一个面积为1的正方形，则该正四棱锥的正视图的面积不可能等于（ ）
| A． | 2 | B． | 2.5 | C． | 2$\sqrt{3}$-1 | D． | 2$\sqrt{2}$+1 |
14．设min{p，q}表示p，q两者中的较小者，若函数f（x）=min{3-x，log2x}，则满足f（x）≤$\frac{1}{2}$的x的集合为（ ）
| A． | （0，2]∪[$\frac{5}{2}$，+∞） | B． | [$\sqrt{2}$，$\frac{5}{2}$] | C． | （0，$\sqrt{2}$]∪[$\frac{5}{2}$，+∞） | D． | （0，$\sqrt{2}$）∪（$\frac{5}{2}$，+∞） |