题目内容
17.已知矩阵A=$[\begin{array}{l}{1}&{2}\\{-1}&{4}\end{array}]$,向量$\overrightarrow{a}$=$[\begin{array}{l}{7}\\{4}\end{array}]$.(1)求A的特征值和对应的特征向量;
(2)计算A5α的值.
分析 (1)通过令矩阵A的特征多项式为f(λ)=0,可得特征值,进而可得对应的特征向量;
(2)通过解方程组α=mα1+nα2,可得m=3,n=1,进而可得结论.
解答 解:(1)矩阵A的特征多项式为f(λ)=$|\begin{array}{l}{λ-1}&{-2}\\{1}&{λ-4}\end{array}|$=λ2-5λ+6=0,
解得:λ1=2,λ2=3,
当λ1=2时,得α1=$[\begin{array}{l}{2}\\{1}\end{array}]$;
当λ2=3时,得α2=$[\begin{array}{l}{1}\\{1}\end{array}]$;
(2)由α=mα1+nα2,可得:$\left\{\begin{array}{l}{2m+n=7}\\{m+n=4}\end{array}\right.$,
解得m=3,n=1,
∴A5α=A5(3α1+α2)=3(A5α1)+A5α2
=3(${{λ}_{1}}^{5}$α1)+${{λ}_{2}}^{5}$α2
=3×25$[\begin{array}{l}{2}\\{1}\end{array}]$+35$[\begin{array}{l}{1}\\{1}\end{array}]$
=$[\begin{array}{l}{435}\\{339}\end{array}]$.
点评 本题考查矩阵的特征值与特征向量的计算,注意解题方法的积累,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.已知全集U=R,集合A={x|y=log2(x-1)},B={y|y=2x},则(∁UA)∩B=( )
| A. | (-∞,0) | B. | (0,1] | C. | (-∞,1) | D. | (1,2) |
9.集合A={-1,0,1,2,3},B={-2,-1,0,1},则图中阴影部分表示的集合为( )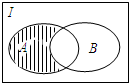

| A. | {-1,0,1} | B. | {2,3} | C. | {-2,2,3} | D. | {-1,0,1,2,3} |
6. 将正奇数组成的数列{an},按下表排成5列:
将正奇数组成的数列{an},按下表排成5列:
(Ⅰ)求第五行到第十行的所有数的和;
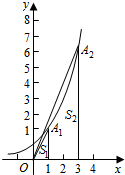
(Ⅱ)已知点A1(a1,b1),A2(a2,b2),…,An(an,bn)在指数函数y=2x的图象上,如果,以A1,A2,…,An为一个顶点,x轴y轴为邻边构成的矩形面积为S1,S2,…Sn,求S1+S2+…+Sn的值Tn.
 将正奇数组成的数列{an},按下表排成5列:
将正奇数组成的数列{an},按下表排成5列:| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 | |
| 第一行 | 1 | 3 | 5 | 7 | |
| 第二行 | 15 | 13 | 11 | 9 | |
| 第三行 | 17 | 19 | 21 | 23 | |
| 第四行 | … | … | 27 | 25 |
(Ⅱ)已知点A1(a1,b1),A2(a2,b2),…,An(an,bn)在指数函数y=2x的图象上,如果,以A1,A2,…,An为一个顶点,x轴y轴为邻边构成的矩形面积为S1,S2,…Sn,求S1+S2+…+Sn的值Tn.
7.已知四面体ABCD的所有顶点都在球O的球面上,球O的半径为2,AB,AC,AD两两垂直,AB=$\sqrt{2}$,则四面体ABCD体积的最大值为( )
| A. | $\frac{7\sqrt{2}}{6}$ | B. | $\frac{7}{3}$ | C. | 2$\sqrt{2}$ | D. | 2 |