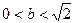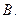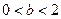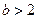题目内容
. (本小题满分13分)
设A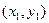 ,B
,B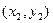 是椭圆
是椭圆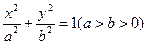 上的两点,
上的两点,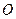 为坐标原点,向量
为坐标原点,向量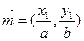 ,向量
,向量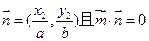 。
。
(1)设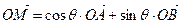 ,证明:点M在椭圆上;
,证明:点M在椭圆上;
(2)若点P、Q为椭圆上两点,且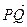 ∥
∥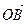 试问:线段PQ能否被直线OA平分?若能平分,请加以证明;若不能平分,请证明理由。
试问:线段PQ能否被直线OA平分?若能平分,请加以证明;若不能平分,请证明理由。
设A
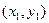 ,B
,B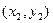 是椭圆
是椭圆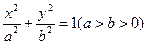 上的两点,
上的两点,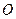 为坐标原点,向量
为坐标原点,向量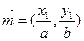 ,向量
,向量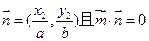 。
。(1)设
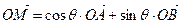 ,证明:点M在椭圆上;
,证明:点M在椭圆上;(2)若点P、Q为椭圆上两点,且
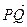 ∥
∥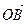 试问:线段PQ能否被直线OA平分?若能平分,请加以证明;若不能平分,请证明理由。
试问:线段PQ能否被直线OA平分?若能平分,请加以证明;若不能平分,请证明理由。(1)
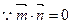
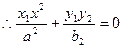 又
又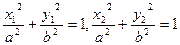
知
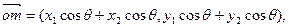 把M点坐标代入椭圆方程左边,
把M点坐标代入椭圆方程左边,得
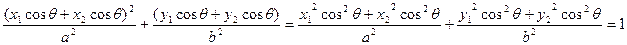
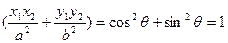 ∴点M在椭圆上。
∴点M在椭圆上。(2)1.若
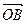 ⊥X轴,则OA在X轴上,由
⊥X轴,则OA在X轴上,由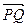 ∥
∥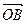 ,∴PQ⊥X轴,∵PQ⊥X轴
,∴PQ⊥X轴,∵PQ⊥X轴∵线段PQ被直线OA平分。
2.若OB∥X轴,同理可证线段PQ被直线OA平分。
2.若
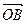 不与X轴垂直或平行,设PQ方程为
不与X轴垂直或平行,设PQ方程为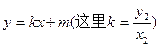
由
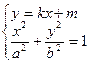
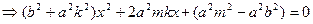
设
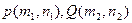 则
则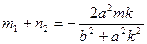
∴
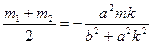 ①
①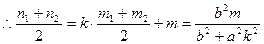 ②
②由①②得PQ中点在直线
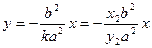 上,
上,又直线OA方程为
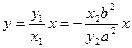
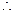 PQ中点在直线OA上,故线段PQ被直线OA平分。
PQ中点在直线OA上,故线段PQ被直线OA平分。略

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
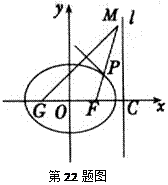
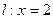 ,设动点P到直线
,设动点P到直线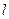 的距离为
的距离为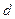 ,已知
,已知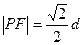 ,且
,且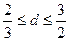 .
.
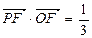 ,求向量
,求向量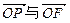 的夹角;
的夹角;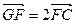 ,点M满足
,点M满足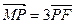 ,且线段MG的垂直平分线经过点P,求
,且线段MG的垂直平分线经过点P,求 的面积.
的面积.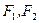 是椭圆
是椭圆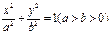 的两个焦点,
的两个焦点, 为坐标原点,点
为坐标原点,点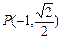 在椭圆上,且
在椭圆上,且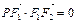 ,⊙
,⊙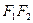 为直径的圆,直线
为直径的圆,直线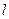 :
: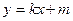 与⊙
与⊙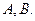
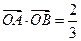 ,求
,求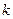 的值.
的值.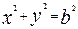 与椭圆
与椭圆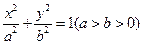 有一个公共点A(0,1),F为椭圆的左焦点,直线AF被圆所截得的弦长为1.
有一个公共点A(0,1),F为椭圆的左焦点,直线AF被圆所截得的弦长为1.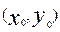 是椭圆上异于点A的一个动点,在线段CD上是否存在点T
是椭圆上异于点A的一个动点,在线段CD上是否存在点T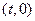 ,使
,使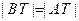 ,若存在,请说明理由。
,若存在,请说明理由。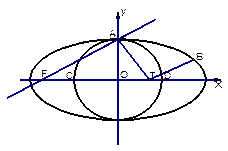
 有共同焦点,且过点
有共同焦点,且过点 的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率.
的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率. 的
的 左焦点为F,右顶点为A,点B在椭圆上,且
左焦点为F,右顶点为A,点B在椭圆上,且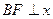 轴,直线AB交
轴,直线AB交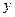 轴于点P。若
轴于点P。若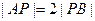 ,则椭圆的离心率为
,则椭圆的离心率为 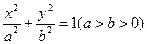 的左右顶点,若在椭圆上存在异于A1、A2的点
的左右顶点,若在椭圆上存在异于A1、A2的点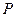 ,使得
,使得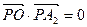 ,其中O为坐标原点,则椭圆的离心率
,其中O为坐标原点,则椭圆的离心率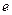 的取值范围是
的取值范围是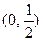
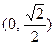
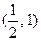
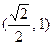
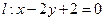 过椭圆左焦点F1和一个顶点B,则该椭圆的离心率为 ( )
过椭圆左焦点F1和一个顶点B,则该椭圆的离心率为 ( )
 在椭圆
在椭圆 内,则
内,则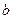 的取值范围为 ( )
的取值范围为 ( )