题目内容
已知圆o: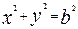 与椭圆
与椭圆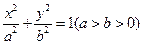 有一个公共点A(0,1),F为椭圆的左焦点,直线AF被圆所截得的弦长为1.
有一个公共点A(0,1),F为椭圆的左焦点,直线AF被圆所截得的弦长为1.
(1)求椭圆方程。
(2)圆o与x轴的两个交点为C、D,B 是椭圆上异于点A的一个动点,在线段CD上是否存在点T
是椭圆上异于点A的一个动点,在线段CD上是否存在点T ,使
,使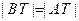 ,若存在,请说明理由。
,若存在,请说明理由。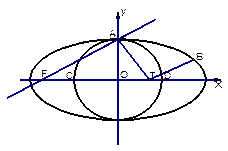
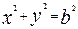 与椭圆
与椭圆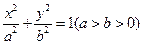 有一个公共点A(0,1),F为椭圆的左焦点,直线AF被圆所截得的弦长为1.
有一个公共点A(0,1),F为椭圆的左焦点,直线AF被圆所截得的弦长为1.(1)求椭圆方程。
(2)圆o与x轴的两个交点为C、D,B
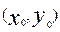 是椭圆上异于点A的一个动点,在线段CD上是否存在点T
是椭圆上异于点A的一个动点,在线段CD上是否存在点T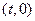 ,使
,使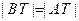 ,若存在,请说明理由。
,若存在,请说明理由。


⑵解法一:假设存在这样的点
 ,使得
,使得 ,则点
,则点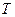 必定在线段
必定在线段 的中垂线上……8分
的中垂线上……8分设点
 ,
,①直线
 斜率存在时,设直线
斜率存在时,设直线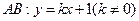
由
 ,
,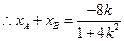 ,
,
则
 的中点
的中点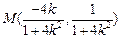 ……………………7分
……………………7分由
 可知
可知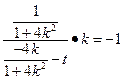 即
即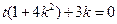
∴
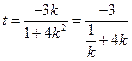
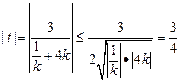 且
且 …………………9分
…………………9分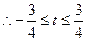 且
且
 ⑵解法二:
⑵解法二: 设
 点B
点B
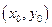 ,由
,由 知
知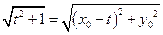
即
 ,整理得
,整理得 ……………7分
……………7分又∵
 ,∴
,∴
当
 时,
时, ;
; 当
 时,
时,
又∵
 ,∴
,∴ ……………10分
……………10分又圆O:

综上可知在线段CD上存在点T,使得
 ……………12分
……………12分略

练习册系列答案
相关题目
 ,B
,B 是椭圆
是椭圆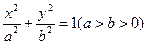 上的两点,
上的两点,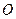 为坐标原点,向量
为坐标原点,向量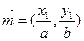 ,向量
,向量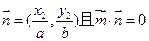 。
。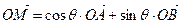 ,证明:点M在椭圆上;
,证明:点M在椭圆上;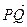 ∥
∥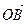 试问:线段PQ能否被直线OA平分?若能平分,请加以证明;若不能平分,请证明理由。
试问:线段PQ能否被直线OA平分?若能平分,请加以证明;若不能平分,请证明理由。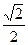 .
.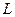 与椭圆交于A、B两点,O为原点,
与椭圆交于A、B两点,O为原点,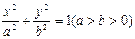 的焦点分别为
的焦点分别为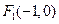 、
、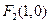 ,直线
,直线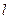 :
: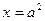 交
交 轴于点
轴于点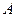 ,且
,且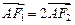 .
.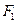 、
、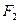 分别作互相垂直的两直线与椭圆分别 交于
分别作互相垂直的两直线与椭圆分别 交于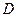 、
、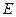 、
、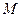 、
、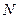 四点(如图所示),试求四边形
四点(如图所示),试求四边形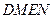 面积的最大值和最小值.
面积的最大值和最小值.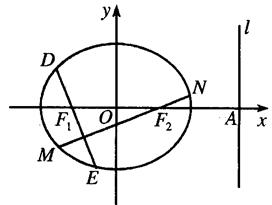
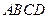 中,
中,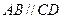 ,且
,且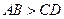 。设以
。设以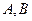 为焦点且过点
为焦点且过点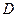 的双曲线的离心率为
的双曲线的离心率为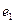 ,以
,以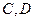 为焦点且过点
为焦点且过点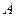 的椭圆的离心率为
的椭圆的离心率为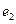 ,则
,则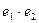 = ;
= ;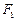 、
、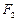 是椭圆
是椭圆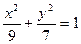 的两个焦点,
的两个焦点,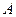 为椭圆上一点,且∠
为椭圆上一点,且∠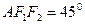 ,则
,则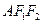 的面积为( )
的面积为( )
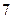 B
B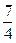 C
C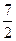 D
D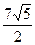
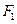 、
、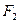 是椭圆
是椭圆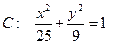 的两个焦点,
的两个焦点,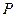 为椭圆上一点,且
为椭圆上一点,且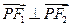 ,若
,若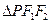 的面积为 .
的面积为 .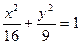 的焦距是 ,焦点坐标为 ;若CD为过左焦点
的焦距是 ,焦点坐标为 ;若CD为过左焦点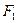 的弦,则
的弦,则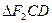 的周长为
的周长为