题目内容
5.已知椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1内有点,P(-1,1),F为椭圆的右焦点,M为椭圆上一点.(1)当MP+2MF取最小值时,求点M的坐标;
(2)当MP+MF取最大值时,求点M的坐标.
分析 (1)利用椭圆的第二定义进行转化,即可求出当MP+2MF取最小值时,求点M的坐标;
(2)利用椭圆的第一定义进行转化,当MP+MF取最大值时,求点M的坐标.
解答 解:(1)∵椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的a=2,b=$\sqrt{3}$,c=1,e=$\frac{1}{2}$.
由题意可得点P在椭圆内部,设M到椭圆的左准线l得距离为d
由椭圆的第二定义可知d=2MF,
∴|PM|+2|MF|=d+|PM|
由题意可得,过P作PN⊥l,当M为该垂线与椭圆的右交点时,所求的值最小,
此时 yM=1,代入可得 xM=$\frac{2\sqrt{6}}{3}$,
故M($\frac{2\sqrt{6}}{3}$,1);
(2)设左焦点为F′,则|MF|+|MF′|=4,∴|MF|=4-|MF′|,
∴|MP|+|MF|=4+|MP|-|MF′|≤4+|PF′|,
直线PF′的方程为x=-1,∴MP+MF取最大值时,点M的坐标是(-1,-$\frac{3}{2}$).
点评 本题考查椭圆的第一、二定义的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
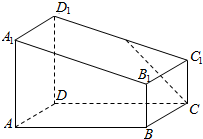 如图所示的一块木料ABCD-A1B1C1D1中,棱AA1,BB1.BB1,DD1互相平行,AA1⊥平面ABCD,四边形ABCD是矩形,AA1=DD1=4,AB=6,BB1=CC1=2,BC=4
如图所示的一块木料ABCD-A1B1C1D1中,棱AA1,BB1.BB1,DD1互相平行,AA1⊥平面ABCD,四边形ABCD是矩形,AA1=DD1=4,AB=6,BB1=CC1=2,BC=4