题目内容
16.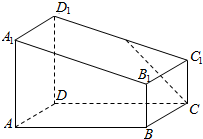 如图所示的一块木料ABCD-A1B1C1D1中,棱AA1,BB1.BB1,DD1互相平行,AA1⊥平面ABCD,四边形ABCD是矩形,AA1=DD1=4,AB=6,BB1=CC1=2,BC=4
如图所示的一块木料ABCD-A1B1C1D1中,棱AA1,BB1.BB1,DD1互相平行,AA1⊥平面ABCD,四边形ABCD是矩形,AA1=DD1=4,AB=6,BB1=CC1=2,BC=4(1)要经过面A1C1的中心M和棱BC讲木料锯开,应怎样画线?在图中作出点M,并画出截线(不必说明画法和理由)
(2)记木料被锯开后的截面为α,求AM与平面α所成的角的正弦值.
分析 (1)注意到棱BC平行于面A′C′,故过点M作B′C′的平行线,交A′B′、C′D′于点E,F,连结BE,CF;
(2)建立空间坐标系,求出AM的方向向量和平面α的法向量,代入向量夹角公式,可得答案.
解答 解:(1)过点M点作B′C′的平行线,
交A′B′、C′D′于点E,F,
连结BE,CF;
作图如右图,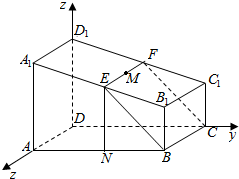
(2)以边DA,DC,DD1所在直线为x,y,z轴,建立如图所示空间直角坐标系,
作EN⊥AB,垂足为N,
∵AA1=DD1=4,AB=6,BB1=CC1=2,BC=4,
则:EN=$\frac{1}{2}$(AA1+BB1)=3,
∴A(4,0,0),M(2,3,3),E(4,3,3),F(0,3,3),B(4,6,0);
∴$\overrightarrow{EF}$=(-4,0,0),$\overrightarrow{EB}$=(0,3,-3),$\overrightarrow{AF}$=(-4,3,3);
设$\overrightarrow{n}$=(x,y,z)为平面α的法向量,
则:$\left\{\begin{array}{l}\overrightarrow{n}⊥\overrightarrow{EF}\\ \overrightarrow{n}⊥\overrightarrow{EB}\end{array}\right.$,即$\left\{\begin{array}{l}\overrightarrow{n}•\overrightarrow{EF}=0\\ \overrightarrow{n}•\overrightarrow{EB}=0\end{array}\right.$,即$\left\{\begin{array}{l}-4x=0\\ 3y-3z=0\end{array}\right.$,
取z=1,则$\overrightarrow{n}$=(0,1,1);
若设直线AM和平面α所成的角为θ,
则:sinθ=|cos<$\overrightarrow{AF}$,$\overrightarrow{n}$>|=$\frac{6}{\sqrt{34}•\sqrt{2}}$=$\frac{3\sqrt{17}}{17}$;
∴直线AM与平面α所成角的正弦值为$\frac{3\sqrt{17}}{17}$
点评 考查直角三角形边的关系,通过建立空间直角坐标系,利用空间向量解决线面角问题的方法,弄清直线和平面所成角与直线的方向向量和平面法向量所成角的关系,以及向量夹角余弦的坐标公式.

| A. | (-∞,+∞) | B. | (-∞,0) | C. | (0,+∞) | D. | 非奇非偶函数 |
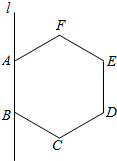 如图所示,ABCDEF是正六边形,将它绕AB所在直线l旋转,画出旋转后的几何体,并指出它是由哪几个简单几何体构成的.
如图所示,ABCDEF是正六边形,将它绕AB所在直线l旋转,画出旋转后的几何体,并指出它是由哪几个简单几何体构成的.