题目内容
若数列{cn}的通项cn=(2n-1)·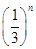 ,则数列{cn}的前n项和Rn=( )
,则数列{cn}的前n项和Rn=( )
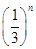 ,则数列{cn}的前n项和Rn=( )
,则数列{cn}的前n项和Rn=( )A.1- | B.1-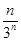 | C.1+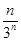 | D.1+ |
A
Rn=c1+c2+c3+…+cn,
Rn=1×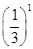 +3×
+3×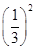 +5×
+5×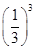 +…+(2n-1)×
+…+(2n-1)×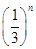 ,①
,①
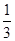 Rn=1×
Rn=1×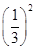 +3×
+3×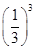 +5×
+5×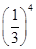 +…+(2n-3)×
+…+(2n-3)×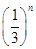 +(2n-1)×
+(2n-1)× ,②
,②
①式减②式得
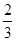 Rn=
Rn=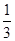 +2
+2 -(2n-1)×
-(2n-1)× ,
,
则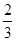 Rn=
Rn=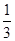 +2×
+2× -(2n-1)×
-(2n-1)× =
=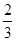 -
-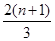 ×
× ,
,
故Rn=1- ,故选A
,故选A
Rn=1×
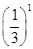 +3×
+3×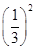 +5×
+5×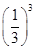 +…+(2n-1)×
+…+(2n-1)×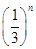 ,①
,①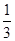 Rn=1×
Rn=1×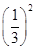 +3×
+3×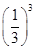 +5×
+5×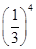 +…+(2n-3)×
+…+(2n-3)×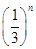 +(2n-1)×
+(2n-1)× ,②
,②①式减②式得
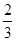 Rn=
Rn=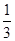 +2
+2 -(2n-1)×
-(2n-1)× ,
,则
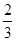 Rn=
Rn=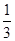 +2×
+2× -(2n-1)×
-(2n-1)× =
=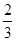 -
-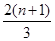 ×
× ,
,故Rn=1-
 ,故选A
,故选A
练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
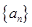 的前
的前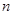 项和为
项和为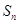 ,且
,且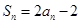 ,
,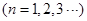 ;数列
;数列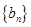 中,
中,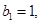 点
点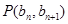 在直线
在直线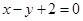 上.
上.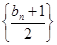 的前
的前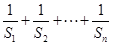 ;
;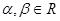 且
且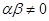 ,数列
,数列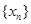 满足
满足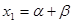 ,
,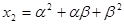 ,
,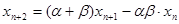 (
(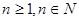 ),令
),令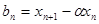 ,
,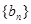 是等比数列;
是等比数列;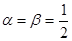 ,求
,求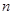 项和
项和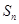 .
.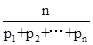 为
为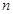 个正数
个正数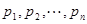 的“均倒数”.若已知数列
的“均倒数”.若已知数列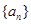 的前
的前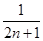 ,又
,又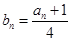 ,则
,则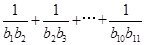 =( )
=( )



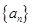 ,其前
,其前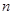 项的和为
项的和为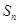 ,且
,且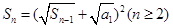 ,若
,若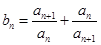 ,且数列
,且数列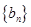 的前
的前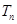 ,则
,则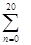 (1+2n)=________.
(1+2n)=________. 的通项公式为
的通项公式为 ,设
,设 ,则当
,则当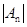 取得最小值是,n的值是 ( )
取得最小值是,n的值是 ( )