题目内容
已知数列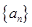 的前
的前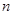 项和为
项和为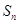 ,且
,且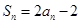 ,
,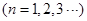 ;数列
;数列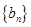 中,
中,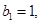 点
点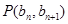 在直线
在直线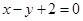 上.
上.
(1)求数列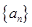 和
和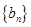 的通项公式;
的通项公式;
(2)设数列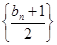 的前
的前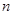 和为
和为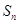 ,求
,求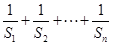 ;
;
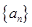 的前
的前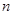 项和为
项和为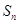 ,且
,且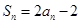 ,
,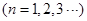 ;数列
;数列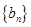 中,
中,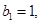 点
点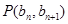 在直线
在直线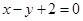 上.
上.(1)求数列
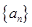 和
和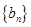 的通项公式;
的通项公式;(2)设数列
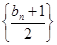 的前
的前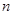 和为
和为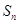 ,求
,求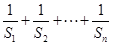 ;
;(1)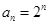 ,
,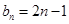 (2)
(2)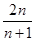
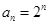 ,
,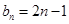 (2)
(2)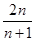
试题分析:(1)求数列
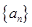 的通项公式用公式法即
的通项公式用公式法即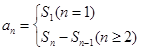 可推导数列
可推导数列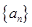 为等比数列,根据等比数列通项公式可求
为等比数列,根据等比数列通项公式可求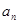 。求
。求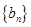 的通项公式也用公式法,根据已知条件可知数列
的通项公式也用公式法,根据已知条件可知数列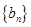 为等差数列,根据等差数列的通项公式可直接求得
为等差数列,根据等差数列的通项公式可直接求得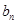 。(2)用列项相消法求和。
。(2)用列项相消法求和。试题解析:解:(1)∵
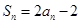 ,
,∴当
 时,
时,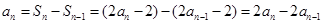 …2分
…2分所以
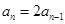 ,即
,即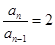
∴数列
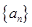 是等比数列.
是等比数列.∵
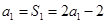 ,∴
,∴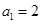
∴
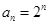 . 5分
. 5分∵点
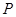
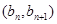 在直线
在直线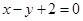 上,
上,∴
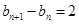 ,
,即数列
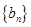 是等差数列,
是等差数列,又
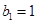 ,∴
,∴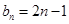 .…7分
.…7分(2)由题意可得
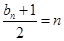 ,∴
,∴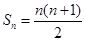 , 9分
, 9分∴
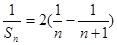 ,…10分
,…10分∴
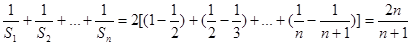 . 14分
. 14分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
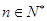 )
)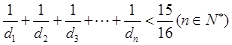 .
.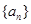 的相邻两项
的相邻两项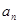 ,
,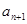 是关于
是关于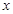 方程
方程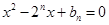 的两根,且
的两根,且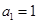 .
.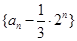 是等比数列;
是等比数列;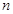 项和
项和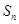 ;
;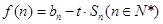 ,若
,若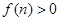 对任意的
对任意的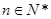 都成立,求实数
都成立,求实数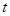 的取值范围.
的取值范围.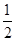 Sn+1(n∈N*);
Sn+1(n∈N*);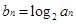 ,cn=
,cn=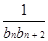 ,且{cn}的前n项和为Tn,求使得
,且{cn}的前n项和为Tn,求使得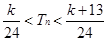 对n∈N*都成立的所有正整数k的值.
对n∈N*都成立的所有正整数k的值.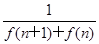 ,n∈N*.记数列{an}的前n项和为Sn,则S2 013=( )
,n∈N*.记数列{an}的前n项和为Sn,则S2 013=( )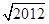 -1
-1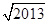 -1
-1 -1
-1 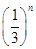 ,则数列{cn}的前n项和Rn=( )
,则数列{cn}的前n项和Rn=( )
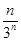
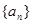 是等和数列,且
是等和数列,且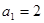 ,公和为5,那么这个数列的前21项和
,公和为5,那么这个数列的前21项和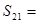 .
.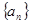 的通项公式
的通项公式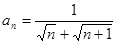 ,则该数列的前_________项之和等于
,则该数列的前_________项之和等于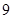 .
. 中,已知
中,已知
 且
且 ,则前
,则前 项和为
项和为 ,则
,则 的值为__________.
的值为__________.