题目内容
12.设集合A={1,2,3},B={2,3,4},C⊆A∩B,则集合C可能是( )| A. | {1,2} | B. | {1,3} | C. | {2,3} | D. | {2,4} |
分析 根据已知,求出A∩B={2,3},若C⊆A∩B,则1∉C,且4∉C,比照四个答案,可得结论.
解答 解:∵集合A={1,2,3},B={2,3,4},
∴A∩B={2,3},
若C⊆A∩B,
则1∉C,且4∉C,
比照四个答案,可得只有C答案满足要求,
故选:C
点评 本题考查的知识点是集合的包含关系判断及应用,集合的交集运算,难度不大,属于基础题.

练习册系列答案
相关题目
3.已知$\vec a$、$\vec b$为两个单位向量,则一定有( )
| A. | $\vec a$=$\vec b$ | B. | $\vec a•\vec b=0$ | C. | $\vec a•\vec b=1$ | D. | $\vec a•\vec a=\vec b•\vec b$ |
1.已知函数f(x)的图象是连续不断的,现给出x,f(x)的部分对应值如下表:
则函数f(x)一定有零点的区间是( )
| x | -2 | -1 | 1 | 2 | 3 |
| f(x) | -3 | -2 | 1 | 2 | 4 |
| A. | (1,2) | B. | (2,3) | C. | (-2,-1) | D. | (-1,1) |
2.已知函数f(x)=|lnx|-k有两个不同的零点a,b,则代数式|$\frac{{a}^{2}+{b}^{2}+2}{a-b}$|的最小值是( )
| A. | 8$\sqrt{2}$ | B. | 8 | C. | 4$\sqrt{2}$ | D. | 4 |
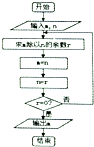 程序框图如图所示,若输入m,n的值分别为30,18,则程序框图中最后输出的m值等于6.
程序框图如图所示,若输入m,n的值分别为30,18,则程序框图中最后输出的m值等于6.