题目内容

10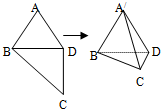．如图所示，在四边形ABCD中，AB=AD=CD=1，BD=$\sqrt{2}$，BD⊥CD，将四边形ABCD沿对角线BD折成四面体A′-BCD，使平面A′BD⊥平面BCD，则下列结论正确的是（2）（4）．
（1）A′C⊥BD；  （2）∠BA′C=90°；
（3）CA′与平面A′BD所成的角为30°；
（4）四面体A′-BCD的体积为$\frac{1}{6}$．

分析 根据题意，依次分析命题：对于（1），可利用反证法说明真假；对于（2），△BA'D为等腰Rt△，CD⊥平面A'BD，得BA'⊥平面A'CD，根据线面垂直可知∠BA′C=90°；对于（3）由CA'与平面A'BD所成的角为∠CA'D=45°知真假；对于（4），利用等体积法求出所求体积进行判定即可，综合可得答案．

解答 解：∵四边形ABCD中，AB=AD=CD=1，BD=$\sqrt{2}$，BD⊥CD，平面A'BD⊥平面BCD，则由A′D与BD不垂直，BD⊥CD，故BD与平面A′CD不垂直，则BD仅于平面A′CD与CD平行的直线垂直，故（1）不正确；
由题设知：△BA'D为等腰Rt△，CD⊥平面A'BD，得BA'⊥平面A'CD，于是（2）正确；
由BD⊥CD，平面A′BD⊥平面BCD，易得CD⊥平面A′BD，∴CD⊥A′B，CD⊥A′D，∵A′D=CD，∴△A′CD为等腰直角三角形，∴∠A′DC=45°，则CA′与平面A′BD所成的角为45°，知（3）不正确；
VA′-BCD=VC-A′BD=$\frac{1}{6}$，故（4）正确．
故答案为：（2）（4）．

点评 本题主要考查了异面直线及其所成的角，以及三棱锥的体积的计算，同时考查了空间想象能力，论证推理能力，解题的关键是须对每一个进行逐一判定．

练习册系列答案
相关题目
20．已知等差数列{an}的前n项和为Sn，且满足S5=5S2，a2n+1=2an+1（n∈N*），正项等比数列{bn}满足b2=a2，b6=a8，数列{cn}满足cn=$\left\{\begin{array}{l}{{a}_{n}，}&{n=2k-1，k∈{N}^{*}}\\{{b}_{n}，}&{n=2k．k∈{N}^{*}}\end{array}\right.$．
（1）求数列{an}，{bn}的通项公式；
（2）求数列{cn}的前n项和为Tn（用n表示）；
（3）是否存在正整数m，使得Tm=2cm+2，若存在，求出所有m的值；若不存在，说明理由．
1．已知函数f（x）的图象是连续不断的，现给出x，f（x）的部分对应值如下表：
x-2-1123
f（x）-3-2124
则函数f（x）一定有零点的区间是（　　）
A．（1，2）B．（2，3）C．（-2，-1）D．（-1，1）
18．已知α，β是两个不同的平面，m，n是两条不同的直线，现给出下列命题：
①若m?α，n?α，m∥β，n∥β，则α∥β；  
②若α⊥β，m?α，则m⊥β；
③若m⊥α，m∥β，则α⊥β；             
④若m∥n，m?α，则n∥α．
其中正确命题的个数是（　　）
A．0B．1C．2D．3
5．已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0）的焦距为2，且过椭圆右焦点F2与上顶点的直线l1与圆O：x2+y2=$\frac{1}{2}$相切．
（1）求椭圆E的方程；
（2）是否存在直线l2，满足l2∥l1，并且l2与椭圆E交于A、B两点，以AB为直径的圆与y轴相切，若存在，请求出l2的方程，若不存在，请说明理由．
15．直线x-ysinθ+1=0（θ∈R）的倾斜角范围是$[\frac{π}{4}，\frac{3π}{4}]$．
2．已知函数f（x）=|lnx|-k有两个不同的零点a，b，则代数式|$\frac{{a}^{2}+{b}^{2}+2}{a-b}$|的最小值是（　　）
A．8$\sqrt{2}$B．8C．4$\sqrt{2}$D．4
15．在平面上，Rt△ABC有勾股定理（即$∠C=\frac{π}{2}$，则有c2=a2+b2），类比到空间中，已知三棱锥P-DEF中，∠PDF=$∠PDE=∠EDF=\frac{π}{2}$，用S1，S2，S3，S分别表示△PDF，△PDE，△EDF，△PEF的面积，则有结论：S2=S12+S22+S32．
16．用数归纳法证明当n为正奇数时，xn+yn能被x+y整除，k∈N*第二步是（　　）
A．设n=2k+1时正确，再推n=2k+3正确
B．设n=2k-1时正确，再推n=2k+1时正确
C．设n=k时正确，再推n=k+2时正确
D．设n≤k（k≥1）正确，再推n=k+2时正确

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网