��Ŀ����
����Ŀ��Ϊ�˽�ѧ��ϲ��У�ڡ�У�չ��������ij��ѧһ����С����ѧУ��һ�꼶�������ʾ����飬�ʾ���100���⣬ÿ��1�֣��ܷ�100�֣��ÿ���С�������ȡ��200��ѧ�����ʾ��ɼ�����λ���֣�����ͳ�ƣ������ݰ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ֳ����飬���Ƶ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ������������60�ֵij�Ϊ
�ֳ����飬���Ƶ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ������������60�ֵij�Ϊ![]() ��ѧ��������60�ֵij�Ϊ
��ѧ��������60�ֵij�Ϊ![]() ��ѧ��.
��ѧ��.

��1��������֪�����������![]() ���������ܷ��ڷ�����ĸ��ʲ�����
���������ܷ��ڷ�����ĸ��ʲ�����![]() ��ǰ������Ϊ�Ա����Ƿ�Ϊ
��ǰ������Ϊ�Ա����Ƿ�Ϊ![]() ��ѧ���й�ϵ��
��ѧ���й�ϵ��
|
| �ϼ� | |
�� | 110 | ||
Ů | 50 | ||
�ϼ� |
��2����Ƶ����Ϊ���ʣ����ڴӸ�У��һѧ��������������ķ���ÿ�γ�ȡ1�ˣ�����ȡ3�Σ��DZ���ȡ��3����![]() ��ѧ��������Ϊ
��ѧ��������Ϊ![]() ����ÿ�γ�ȡ�Ľ����������ģ���
����ÿ�γ�ȡ�Ľ����������ģ���![]() �ķֲ��С�����
�ķֲ��С�����![]() �ͷ���
�ͷ���![]() .
.
�ο���ʽ��![]() ������
������![]() .
.
�ο��ٽ�ֵ��
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���𰸡�(1)������������; �ڷ�����ĸ��ʲ�����0.01��ǰ������Ϊ�Ա���![]() ��ѧ���й�.
��ѧ���й�.
(2)�ֲ��м�����;![]() ;
;![]() .
.
����������������1����Ƶ�ʷֲ�ֱ��ͼ�ɵ÷�����![]() ��
��![]() ֮���ѧ���������ó�
֮���ѧ���������ó�![]() �������������ù�ʽ�����
�������������ù�ʽ�����![]() �Ĺ۲�ֵ�����������жϣ�
�Ĺ۲�ֵ�����������жϣ�
��2����֪�Ӹ�У��һѧ���������ȡ1�ˣ����ѧ��Ϊ��![]() �ࡱ�ĸ���Ϊ
�ࡱ�ĸ���Ϊ![]() �������õ�
�������õ�![]() �����ö���ֲ���÷ֲ��У���������ѧ������
�����ö���ֲ���÷ֲ��У���������ѧ������
��⣺��1����Ƶ�ʷֲ�ֱ��ͼ�ɵ÷�����![]() ֮���ѧ������Ϊ
֮���ѧ������Ϊ![]() ����
����![]() ֮���ѧ������Ϊ
֮���ѧ������Ϊ![]() �����Ե���60�ֵ�ѧ������Ϊ120.���������Ϊ��
�����Ե���60�ֵ�ѧ������Ϊ120.���������Ϊ��
|
| �ϼ� | |
�� | 80 | 30 | 110 |
Ů | 40 | 50 | 90 |
�ϼ� | 120 | 80 | 200 |
��![]() �Ĺ۲�ֵΪ
�Ĺ۲�ֵΪ![]()
![]() ��
��
�����ڷ�����ĸ��ʲ�����0.01��ǰ������Ϊ�Ա���![]() ��ѧ���й�.
��ѧ���й�.
��2����֪�Ӹ�У��һѧ���������ȡ1�ˣ����ѧ��Ϊ��![]() �ࡱ�ĸ���Ϊ
�ࡱ�ĸ���Ϊ![]() .
.
������֪![]() ��
��
����![]()
![]() ��
��
����![]() �ķֲ���Ϊ
�ķֲ���Ϊ
| 0 | 1 | 2 | 3 |
|
|
|
|
|
��������![]() ������
������![]() .
.

 ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д�
ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д�����Ŀ��Ϊ�˼��ij�������һ�������ߵ��������̣�����Աÿ��Ӹ��������������ȡ16���������������ߴ磨��λ��cm�������ݳ����������飬������Ϊ��������������״̬������������ijߴ������̬�ֲ�N���̣���2������12�֣�
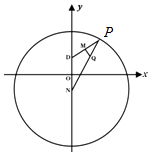
��1����������״̬��������X��ʾһ���ڳ�ȡ��16���������ߴ��ڣ��̩�3�ң���+3�ң�֮������������P��X��1����X����ѧ������
��2��һ���ڳ������У���������˳ߴ��ڣ��̩�3�ң���+3�ң�֮������������Ϊ��������������һ����������̿��ܳ������쳣�������Ե�����������̽��м�飮
��������˵����������������̷����ĺ����ԣ�
�����������Ǽ���Ա��һ���ڳ�ȡ��16������ijߴ磺
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
������� ![]() =
= ![]() =9.97��s=
=9.97��s= ![]() =
= ![]() ��0.212������xiΪ��ȡ�ĵ�i������ijߴ磬i=1��2������16��
��0.212������xiΪ��ȡ�ĵ�i������ijߴ磬i=1��2������16��
������ƽ���� ![]() ��Ϊ�̵Ĺ���ֵ
��Ϊ�̵Ĺ���ֵ ![]() ������������s��Ϊ�ҵĹ���ֵ
������������s��Ϊ�ҵĹ���ֵ ![]() �����ù���ֵ�ж��Ƿ���Ե�����������̽��м�飿����
�����ù���ֵ�ж��Ƿ���Ե�����������̽��м�飿���� ![]() ��3
��3 ![]() +3
+3 ![]() ��֮������ݣ���ʣ�µ����ݹ��Ʀ̺ͦң���ȷ��0.01����
��֮������ݣ���ʣ�µ����ݹ��Ʀ̺ͦң���ȷ��0.01����
�������������Z������̬�ֲ�N���̣���2������P���̩�3�ң�Z����+3�ң�=0.9974��0.997416��0.9592�� ![]() ��0.09��
��0.09��
����Ŀ��ij��ѧ�ߵ���ѧ��ʦ��ѧ�ڷֱ���![]() ���ֲ�ͬ�Ľ�ѧ��ʽ����ס���������һ�°ࣨ������Ϊ60�ˣ���ѧ��ѧƽ�������������ʶ���ͬ���ڷ̶ܳȺ��Ծ��Զ�һ�������������ȡ�ס��������20���ĸߵ���ѧ��ĩ���Գɼ����õ���Ҷͼ��
���ֲ�ͬ�Ľ�ѧ��ʽ����ס���������һ�°ࣨ������Ϊ60�ˣ���ѧ��ѧƽ�������������ʶ���ͬ���ڷ̶ܳȺ��Ծ��Զ�һ�������������ȡ�ס��������20���ĸߵ���ѧ��ĩ���Գɼ����õ���Ҷͼ��

����������Ҷͼ�ж��ĸ����ƽ���ָߣ�
��������������ߵ���ѧ�ɼ����õ���80�ֵ�ͬѧ�������ȡ����ͬѧ����ɼ�Ϊ86�ֵ�ͬѧ������һ�������еĸ��ʣ�
������ѧУ�涨���ɼ�������85�ֵ�Ϊ���㣬����д�����![]() �����������ж����ܷ��ڷ�����ĸ��ʲ�����0.025��ǰ������Ϊ�ɼ��������ѧ��ʽ�йأ���
�����������ж����ܷ��ڷ�����ĸ��ʲ�����0.025��ǰ������Ϊ�ɼ��������ѧ��ʽ�йأ���
�װ� | �Ұ� | �ϼ� | |
���� | |||
������ | |||
�ϼ� |
�����ٽ�ֵ�������ο���
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���ο���ʽ��![]() ����
����![]() ��
��