[题目]如图.已知圆N:x2+(y+ )2=36.P是圆N上的点.点Q在线段NP上.且有点D(0. )和DP上的点M.满足 =2 . =0． (1)当P在圆上运动时.求点Q的轨迹方程,(2)若斜率为的直线l与(1)中所求Q的轨迹交于不同两点A.B.又点C( .2).求△ABC面积最大值时对应的直线l的方程．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，已知圆N：x2+（y+ ）2=36，P是圆N上的点，点Q在线段NP上，且有点D（0，）和DP上的点M，满足 =2 ， =0．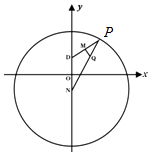
（1）当P在圆上运动时，求点Q的轨迹方程；
（2）若斜率为的直线l与（1）中所求Q的轨迹交于不同两点A、B，又点C（，2），求△ABC面积最大值时对应的直线l的方程．

【答案】
（1）解：由题意，MQ是线段DP的中垂线，∴|NP|=|NQ|+|QP|=|QN|+|QD|=6＞|DN|=2 ，

∴Q的轨迹是以D，N为焦点的椭圆，且c= ，a=3，b=2，

∴求点Q的轨迹方程是 =1

（2）解：设l：y= x+m，A（x1，y1），B（x2，y2），

与椭圆联立，可得9x2+6mx+2m2﹣18=0，

x1+x2=﹣ m，x1x2= （2m2﹣18），

|AB|= = ，

C（，2）到直线l的距离d= ，

S= = ，

∴m=±3时，S最大，此时直线l的方程为y= x±3

【解析】（1）当P在圆上运动时，利用椭圆的定义，求点Q的轨迹方程；（2）△ABC的面积取到最大值问题，要先建立关于某个自变量的函数，后再求此函数的最大值即可．

练习册系列答案

相关题目

【题目】[选修4-5：不等式选讲]
已知函数f（x）=﹣x2+ax+4，g（x）=|x+1|+|x﹣1|．（10分）
（1）当a=1时，求不等式f（x）≥g（x）的解集；
（2）若不等式f（x）≥g（x）的解集包含[﹣1，1]，求a的取值范围．

【题目】在直角坐标系中，曲线的参数方程为（为参数），直线的参数方程为（为参数），且直线与曲线交于两点，以直角坐标系的原点为极点，以轴的正半轴为极轴建立极坐标系.

（1）求曲线的极坐标方程；

（2）已知点的极坐标为，求的值

【题目】在中，分别为内角的对边，且

(1)求角的大小；

(2)若求的值。

【题目】已知函数f（x）g（x）分别是定义在R上的偶函数和奇函数，且f（x）+g（x）=23x．

（1）证明：f（x）-g（x）=23-x，并求函数f（x），g（x）的解析式；

（2）解关于x不等式：g（x2+2x）+g（x-4）＞0；

（3）若对任意x∈R，不等式f（2x）≥mf（x）-4恒成立，求实数m的最大值．

【题目】已知函数

(1)当时，讨论函数零点的个数；

(2)若，当=1时，求证：

【题目】某大学开设甲、乙、丙三门选修课，学生是否选修哪门课互不影响，已知某学生只选修甲的概率为0.08，只选修甲和乙的概率是0.12，至少选修一门的概率是0.88，用表示该学生选修的课程门数和没有选修的课程门数的乘积．

（1）记“函数为上的偶函数”为事件，求事件的概率；

（2）求的分布列和数学期望．

【题目】为了解学生喜欢校内、校外开展活动的情况，某中学一课外活动小组在学校高一年级进行了问卷调查，问卷共100道题，每题1分，总分100分，该课外活动小组随机抽取了200名学生的问卷成绩（单位：分）进行统计，将数据按，，，，分成五组，绘制的频率分布直方图如图所示，若将不低于60分的称为类学生，低于60分的称为类学生.