Question

【题目】已知二次函数f（x）=ax2+bx，（a，b为常数，且a≠0）满足条件f（2-x）=f（x-1），且方程f（x）=x有两个相等的实根．

（1）求f（x）的解析式；

（2）设g（x）=kx+1，若F（x）=g（x）-f（x），求F（x）在[1，2]上的最小值；

（3）是否存在实数m，n（m＜n），使f（x）的定义域和值域分别为[m，n]与[2m，2n]，若存在，求出m，n的值，若不存在，请说明理由．

Answer 1

【答案】（1）f（x）=-x2+x（2）F（x）min=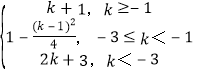（3）

【解析】

（1）结合一元二次函数的图形特征，列出与△=0；（2）根据对称轴与区间的关系来分类讨论；
（3）观察图形知 ；f（x）在[m，n]上单调递增

（1）由题意知f（x）=ax2+bx关于x=对称

∴-=

ax2+bx=x有两个相等的实根，∴△=0

∴

所以，f（x）=-x2+x；

（2）F（x）=kx+1+x2-x=x2+（k-1）x+1

F（x）的对称轴为：x=-

①当-≤1时，F（x）min=F（1）≤k+1

②当1＜-≤2时，

③当-＞2时，F（x）min=F（2）=2k+3

∴F（x）min=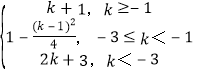

（3）f（x）=

∴2nn

∴f（x）在[m，n]上单调递增

∴

∵m＜n ∴