题目内容
设数列{an}的各项均为正数.若对任意的n∈N*,存在k∈N*,使得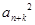 =an·an+2k成立,则称数列{an}为“Jk型”数列.
=an·an+2k成立,则称数列{an}为“Jk型”数列.
(1)若数列{an}是“J2型”数列,且a2=8,a8=1,求a2n;
(2)若数列{an}既是“J3型”数列,又是“J4型”数列,证明:数列{an}是等比数列.
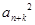 =an·an+2k成立,则称数列{an}为“Jk型”数列.
=an·an+2k成立,则称数列{an}为“Jk型”数列.(1)若数列{an}是“J2型”数列,且a2=8,a8=1,求a2n;
(2)若数列{an}既是“J3型”数列,又是“J4型”数列,证明:数列{an}是等比数列.
(1)a2n=a2qn-1=(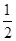 )n-4.
)n-4.
(2)见解析
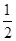 )n-4.
)n-4.(2)见解析
解:(1)由题意得a2,a4,a6,a8,…成等比数列,且公比q=(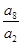 )
)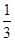 =
=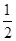 ,
,
所以a2n=(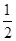 )n-4.
)n-4.
(2)由数列{an}是“J4型”数列,得
a1,a5,a9,a13,a17,a21,…成等比数列,设公比为t.
由数列{an}是“J3型”数列,得
a1,a4,a7,a10,a13,…成等比数列,设公比为α1;
a2,a5,a8,a11,a14,…成等比数列,设公比为α2;
a3,a6,a9,a12,a15,…成等比数列,设公比为α3.
则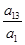 =α14=t3,
=α14=t3,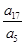 =α24=t3,
=α24=t3,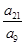 =α34=t3.
=α34=t3.
所以α1=α2=α3,不妨记α=α1=α2=α3,且t=α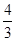 .
.
于是a3k-2=a1αk-1=a1(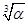 )(3k-2)-1,
)(3k-2)-1,
a3k-1=a5αk-2=a1tαk-2=a1αk-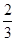 =a1(
=a1(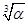 )(3k-1)-1,
)(3k-1)-1,
a3k=a9αk-3=a1t2αk-3=a1αk-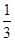 =a1(
=a1(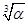 )3k-1,
)3k-1,
所以an=a1(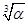 )n-1,故{an}为等比数列.
)n-1,故{an}为等比数列.
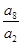 )
)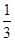 =
=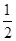 ,
,所以a2n=(
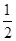 )n-4.
)n-4.(2)由数列{an}是“J4型”数列,得
a1,a5,a9,a13,a17,a21,…成等比数列,设公比为t.
由数列{an}是“J3型”数列,得
a1,a4,a7,a10,a13,…成等比数列,设公比为α1;
a2,a5,a8,a11,a14,…成等比数列,设公比为α2;
a3,a6,a9,a12,a15,…成等比数列,设公比为α3.
则
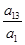 =α14=t3,
=α14=t3,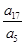 =α24=t3,
=α24=t3,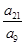 =α34=t3.
=α34=t3.所以α1=α2=α3,不妨记α=α1=α2=α3,且t=α
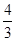 .
.于是a3k-2=a1αk-1=a1(
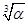 )(3k-2)-1,
)(3k-2)-1,a3k-1=a5αk-2=a1tαk-2=a1αk-
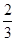 =a1(
=a1(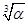 )(3k-1)-1,
)(3k-1)-1,a3k=a9αk-3=a1t2αk-3=a1αk-
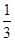 =a1(
=a1(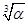 )3k-1,
)3k-1,所以an=a1(
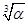 )n-1,故{an}为等比数列.
)n-1,故{an}为等比数列.
练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
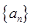 中,
中,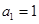 ,前
,前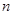 项的和是
项的和是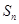 ,且
,且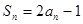 ,
,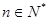 .
.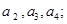
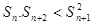 .
.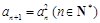 ,则数列的通项公式 .
,则数列的通项公式 .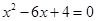 的两根的等比中项是( )
的两根的等比中项是( )



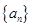 中,
中, 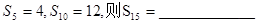
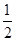 a3,a1成等差数列,则
a3,a1成等差数列,则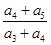 =( )
=( )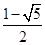
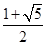
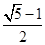
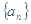 是公比为2的等比数列,若
是公比为2的等比数列,若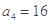 ,则
,则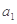 = ( )
= ( )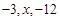 成等比数列,该数列公比q= ___________.
成等比数列,该数列公比q= ___________.