题目内容
已知数列{an}是一个公差大于0的等差数列,且满足a3a6=55,a2+a7=16
(1)求数列{an}的通项公式;
(2)数列{an}和数列{bn}满足等式an=
+
+
+…+
(n∈N*),求数列{bn}的前n项和Sn.
(1)求数列{an}的通项公式;
(2)数列{an}和数列{bn}满足等式an=
| b1 |
| 2 |
| b2 |
| 22 |
| b3 |
| 23 |
| bn |
| 2n |
(1)设等差数列{an}的公差为d,
则依题意可知d>0由a2+a7=16,
得2a1+7d=16①
由a3a6=55,得(a1+2d)(a1+5d)=55②
由①②联立方程求得
得d=2,a1=1或d=-2,a1=
(排除)
∴an=1+(n-1)•2=2n-1
(2)令cn=
,则有an=c1+c2+…+cn
an+1=c1+c2+…+cn+1
两式相减得
an+1-an=cn+1,由(1)得a1=1,an+1-an=2
∴cn+1=2,即cn=2(n≥2),
即当n≥2时,
bn=2n+1,又当n=1时,b1=2a1=2
∴bn=
于是Sn=b1+b2+b3+…+bn=2+23+24+…2n+1=2n+2-6,n≥2,
Sn=
.
则依题意可知d>0由a2+a7=16,
得2a1+7d=16①
由a3a6=55,得(a1+2d)(a1+5d)=55②
由①②联立方程求得
得d=2,a1=1或d=-2,a1=
| 20 |
| 7 |
∴an=1+(n-1)•2=2n-1
(2)令cn=
| bn |
| 2n |
an+1=c1+c2+…+cn+1
两式相减得
an+1-an=cn+1,由(1)得a1=1,an+1-an=2
∴cn+1=2,即cn=2(n≥2),
即当n≥2时,
bn=2n+1,又当n=1时,b1=2a1=2
∴bn=
|
于是Sn=b1+b2+b3+…+bn=2+23+24+…2n+1=2n+2-6,n≥2,
Sn=
|

练习册系列答案
相关题目
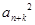 =an·an+2k成立,则称数列{an}为“Jk型”数列.
=an·an+2k成立,则称数列{an}为“Jk型”数列.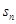 为等比数列
为等比数列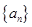 的前n项和,已知
的前n项和,已知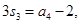
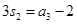 ,则公比q = ( ).
,则公比q = ( ).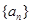 的前
的前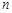 项和为
项和为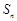 ,且
,且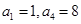 ,则
,则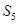 = .
= .