Question

【题目】矩形ABCD中，AD=2，AB=4，E，F分别为边AB，AD的中点，将△ADE沿DE折起，点A，F折起后分别为点A′，F′，得到四棱锥A′﹣BCDE．给出下列几个结论：
①A′，B，C，F′四点共面；
②EF'∥平面A′BC；
③若平面A′DE⊥平面BCDE，则CE⊥A′D；
④四棱锥A′﹣BCDE体积的最大值为 ．
其中正确的是（填上所有正确的序号）．

Answer 1

【答案】②③
【解析】解：由题意知，矩形ABCD折叠后的图 由图可知，F'点不在平面A'BC上，因此四点不共面，①说法错误；去A'C中点为G，连接F'G，GB，F'E如图 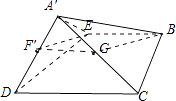所以F'G为三角形A'DC的中位线，∵DC=2EB=2F'G∴F'G平行且等于EB，四边形F'EBG是平行四边形，∴EF'∥GB，GB面A'BC，②正确；∵AB=2AD，∴DE⊥CE，DE为垂线，由面面垂直结论，CE⊥面A'DE，③正确；当面A'DE旋转到与底面垂直时体积最大，为2 ．
所以答案是：②③．
【考点精析】解答此题的关键在于理解棱柱的结构特征的相关知识，掌握两底面是对应边平行的全等多边形；侧面、对角面都是平行四边形；侧棱平行且相等；平行于底面的截面是与底面全等的多边形．