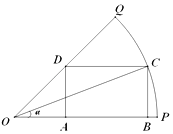
题目内容
【题目】在极坐标系中,圆![]() 的极坐标方程为
的极坐标方程为![]() ,若以极点
,若以极点![]() 为原点,极轴所在的直线为
为原点,极轴所在的直线为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(1)求圆![]() 的参数方程;
的参数方程;
(2)在直线坐标系中,点![]() 是圆
是圆![]() 上的动点,试求
上的动点,试求![]() 的最大值,并求出此时点
的最大值,并求出此时点![]() 的直角坐标.
的直角坐标.
【答案】(1)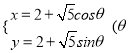 为参数)(2)
为参数)(2)![]() 的最大值为
的最大值为![]() 时,点
时,点![]() 的直角坐标为
的直角坐标为![]() .
.
【解析】试题分析:(1)极坐标转化为参数方程,先化为标准方程,再化为参数方程,利用![]() ,
, ![]() 解题;(2)设
解题;(2)设![]() ,代入圆
,代入圆![]() ,得到
,得到![]() 的最大值为
的最大值为![]() ,点
,点![]() 的直角坐标为
的直角坐标为![]() .
.
试题解析:
解:(1)因为![]() ,所以
,所以![]() ,
,
即![]() 为圆
为圆![]() 的直角坐标方程,
的直角坐标方程,
所以圆![]() 的参数方程为
的参数方程为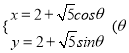 为参数).
为参数).
(2)设![]() ,得
,得![]() ,
,
代入![]() ,整理得
,整理得![]() ,
,
则关于![]() 的方程必有实数根,所以
的方程必有实数根,所以![]() ,
,
化简得![]() ,解得
,解得![]() ,即
,即![]() 的最大值为
的最大值为![]() ,
,
将![]() 代入方程得
代入方程得![]() ,
,
解得![]() ,代入
,代入![]() ,得
,得![]() ,
,
故![]() 的最大值为
的最大值为![]() 时,点
时,点![]() 的直角坐标为
的直角坐标为![]() .
.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目