题目内容
17.关于x的不等式(ax+b)(x-2)>0(b>0)的解集为A,记满足(1,2)⊆A的有序实数对(a,b)构成集合N,若向集合M={(a,b)|-1<a<0,0<b<2}所在平面区域内投掷一质点,质点等可能地落在M内任意一点,则该质点恰好落在集合N所在区域内的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{6}$ |
分析 根据一元二次不等式的性质以及集合的关系求出集合N满足的条件,作出不等式组对应的平面区域求出对应区域的面积,根据几何概型的概率公式进行求解即可.
解答 解:∵满足(1,2)⊆A的有序实数对(a,b)构成集合N,
∴则a<0,设f(x)=(ax+b)(x-2),
则满足$\left\{\begin{array}{l}{f(1)=(a+b)(1-2)≥0}\\{f(2)=0≥0}\end{array}\right.$,
即$\left\{\begin{array}{l}{a<0}\\{a+b≤0}\end{array}\right.$,∵b>0,∴$\left\{\begin{array}{l}{a<0}\\{b>0}\\{a+b≤0}\end{array}\right.$,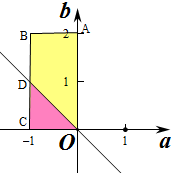
作出不等式组对应的平面区域如图:
则M对应的区域为矩形OABC,面积S=2,
N对应的区域为△OCD,面积S=$\frac{1}{2}×1×1=\frac{1}{2}$,
则该质点恰好落在集合N所在区域内的概率为P=$\frac{\frac{1}{2}}{2}$=$\frac{1}{4}$,
故选:B
点评 本题主要考查几何概型的概率的计算,根据一元二次不等式以及集合关系求出集合N的等价条件是解决本题的关键.

练习册系列答案
相关题目
7.有一个7人学习合作小组,从中选取4人发言,要求其中组长和副组长至少有一人参加,若组长和副组长同时参加,则他们发言时顺序不能相邻,那么不同的发言顺序有( )
| A. | 720种 | B. | 600种 | C. | 360种 | D. | 300种 |
9.已知复数z=(1-i)(1+2i),其中i为虚数单位,则$\overline{z}$的虚部为( )
| A. | -i | B. | 1 | C. | -1 | D. | i |
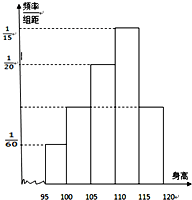 某幼儿园中班共36个小朋友的身高(单位:厘米)测量结果如下频率
某幼儿园中班共36个小朋友的身高(单位:厘米)测量结果如下频率