题目内容
12．
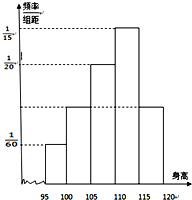某幼儿园中班共36个小朋友的身高（单位：厘米）测量结果如下频率分布直方图所示，该班小朋友牛牛的身高118cm，他所在的身高段共有6个小朋友．
分析 根据频率分布直方图，利用频率和为1，求出身高在115～120cm内的频率与频数即可．
解答 解：根据频率分布直方图，得；
身高在100～105cm和身高在115～120cm内的数据频率相等，
根据频率和为1，得；
身高在115～120cm内的数据频率为
$\frac{1}{2}$[1-（$\frac{1}{60}$+$\frac{1}{20}$+$\frac{1}{15}$）×5]=$\frac{1}{6}$，
所以，身高在115～120cm内的频数为
36×$\frac{1}{6}$=6．
故答案为：6．
点评 本题考查了频率分布直方图的应用问题，也考查了频率、频数与样本容量的关系，是基础题目．
练习册系列答案
相关题目
2．设集合A={x∈N|y=ln（2-x）}，B={x|x（x-1）≤0}，则A∩B=（ ）
| A． | {x|x≥1} | B． | {x|1≤x＜2} | C． | {1} | D． | {0，1} |
20．已知集合 A={x∈R|x-1≥0}，B={x∈R||x|≤2}，则A∩B=（ ）
| A． | {x∈R|-2≤x≤2} | B． | {x∈R|-1≤x≤2} | C． | {x∈R|1≤x≤2} | D． | {x∈R|-1≤x≤1} |
7．已知C，D是圆A：（x+1）2+y2=1与圆B：x2+（y-2）2=4的公共点，则△BCD的面积为（ ）
| A． | $\frac{4}{5}$ | B． | $\frac{8}{5}$ | C． | $\frac{{4\sqrt{5}}}{5}$ | D． | $\frac{{8\sqrt{5}}}{5}$ |
17．关于x的不等式（ax+b）（x-2）＞0（b＞0）的解集为A，记满足（1，2）⊆A的有序实数对（a，b）构成集合N，若向集合M={（a，b）|-1＜a＜0，0＜b＜2}所在平面区域内投掷一质点，质点等可能地落在M内任意一点，则该质点恰好落在集合N所在区域内的概率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{8}$ | D． | $\frac{1}{6}$ |
4．已知互不相等的正数a，b，c，d，p，q满足a，c，b，d成等差数列，a，p，b，q成等比数列，则（ ）
| A． | c＜p，d＞q | B． | c＞p，d＞q | C． | c＞p，d＜q | D． | c＜p，d＜q |
某同学做了一个如图所示的等腰直角三角形形状的数表，且把奇数和偶数分别依次排在了数表的奇数行和偶数行，若用a（i，j）表示第i行从左数第j个数，如a（4，3）=10，则a（21，6）=（ ）