题目内容
9．已知复数z=（1-i）（1+2i），其中i为虚数单位，则$\overline{z}$的虚部为（ ）| A． | -i | B． | 1 | C． | -1 | D． | i |
分析 利用复数的运算法则、虚部的定义即可得出．
解答 解：∵复数z=（1-i）（1+2i）=3+i，
∴$\overline{z}$=3-i的虚部为-1．
故选：C．
点评 本题考查了复数的运算法则、虚部的定义，属于基础题．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
19．
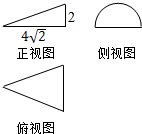一个几何体的三视图及尺寸如图所示，其中正视图是直角三角形，侧视图是半圆，俯视图是等腰三角形，该几何体的体积为（ ）
一个几何体的三视图及尺寸如图所示，其中正视图是直角三角形，侧视图是半圆，俯视图是等腰三角形，该几何体的体积为（ ）| A． | $\frac{8\sqrt{2}π}{3}$ | B． | $\frac{16\sqrt{2}π}{3}$ | C． | 4$\sqrt{2}π$ | D． | 8$\sqrt{2}π$ |
20．已知集合 A={x∈R|x-1≥0}，B={x∈R||x|≤2}，则A∩B=（ ）
| A． | {x∈R|-2≤x≤2} | B． | {x∈R|-1≤x≤2} | C． | {x∈R|1≤x≤2} | D． | {x∈R|-1≤x≤1} |
17．关于x的不等式（ax+b）（x-2）＞0（b＞0）的解集为A，记满足（1，2）⊆A的有序实数对（a，b）构成集合N，若向集合M={（a，b）|-1＜a＜0，0＜b＜2}所在平面区域内投掷一质点，质点等可能地落在M内任意一点，则该质点恰好落在集合N所在区域内的概率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{8}$ | D． | $\frac{1}{6}$ |
4．已知互不相等的正数a，b，c，d，p，q满足a，c，b，d成等差数列，a，p，b，q成等比数列，则（ ）
| A． | c＜p，d＞q | B． | c＞p，d＞q | C． | c＞p，d＜q | D． | c＜p，d＜q |
17．已知实数x，y满足条件$\left\{\begin{array}{l}2x+y≥4\\ x-y≥1\\ x-2y≤2\end{array}\right.$，则z=x+2y的最小值为（ ）
| A． | $\frac{4}{3}$ | B． | 4 | C． | 2 | D． | 3 |