题目内容
(本小题满分14分)
在平面直角坐标系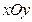 中,已知椭圆
中,已知椭圆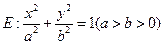 过点
过点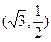 ,且椭圆
,且椭圆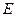 的离心率为
的离心率为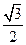
(1)求椭圆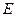 的方程
的方程
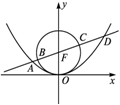
(2)是否存在以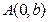 为直角顶点且内接于椭圆
为直角顶点且内接于椭圆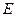 的等腰直角三角形?
的等腰直角三角形? 若存在,求出共有几个;若不存在,请说明理由
若存在,求出共有几个;若不存在,请说明理由
在平面直角坐标系
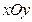 中,已知椭圆
中,已知椭圆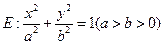 过点
过点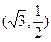 ,且椭圆
,且椭圆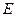 的离心率为
的离心率为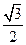
(1)求椭圆
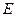 的方程
的方程(2)是否存在以
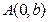 为直角顶点且内接于椭圆
为直角顶点且内接于椭圆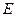 的等腰直角三角形?
的等腰直角三角形? 若存在,求出共有几个;若不存在,请说明理由
若存在,求出共有几个;若不存在,请说明理由解:(1)由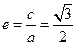 得
得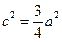 , …1分
, …1分
又 . …2分
. …2分
故椭圆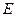 方程为
方程为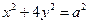 ,
,
椭圆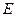 经过点
经过点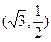 ,则
,则
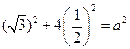 .
.  …3分
…3分
所以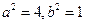 … 4分
… 4分
所以椭圆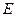 的标准方程为
的标准方程为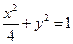 . …5分
. …5分
(2)假设存在这样的等腰直角三角形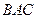 .
.
明显直线 的斜率存在,因为
的斜率存在,因为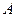 点的坐标为
点的坐标为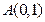 ,设直线
,设直线 的方程
的方程 ,则直线
,则直线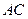 的方程为
的方程为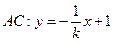 . …6分
. …6分
由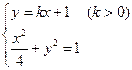 得
得
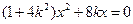
所以 ,或
,或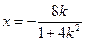 [
[
所以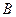 点的纵坐标为
点的纵坐标为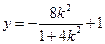 …7分
…7分
所以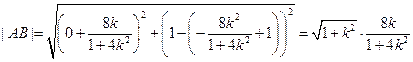 .…8分
.…8分
同理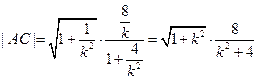 …9分[
…9分[
因为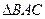 是等腰直角三角形,所以
是等腰直角三角形,所以 ,即
,即
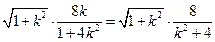 …10分
…10分
即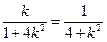
所以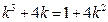 ,即
,即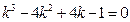 …11分
…11分
所以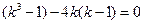
即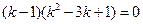
所以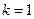 ,或
,或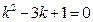 …12分
…12分
所以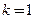 ,或
,或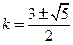 . …13分
. …13分
所以这样的直角三角形有三个. …14分
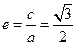 得
得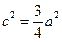 , …1分
, …1分又
 . …2分
. …2分故椭圆
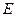 方程为
方程为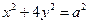 ,
,椭圆
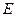 经过点
经过点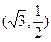 ,则
,则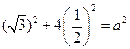 .
.  …3分
…3分所以
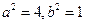 … 4分
… 4分所以椭圆
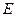 的标准方程为
的标准方程为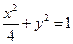 . …5分
. …5分(2)假设存在这样的等腰直角三角形
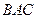 .
.明显直线
 的斜率存在,因为
的斜率存在,因为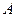 点的坐标为
点的坐标为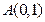 ,设直线
,设直线 的方程
的方程 ,则直线
,则直线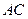 的方程为
的方程为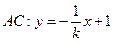 . …6分
. …6分由
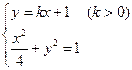 得
得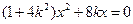
所以
 ,或
,或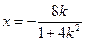 [
[所以
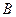 点的纵坐标为
点的纵坐标为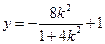 …7分
…7分所以
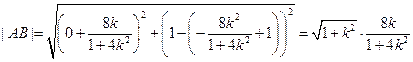 .…8分
.…8分同理
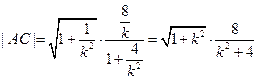 …9分[
…9分[因为
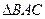 是等腰直角三角形,所以
是等腰直角三角形,所以 ,即
,即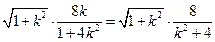 …10分
…10分即
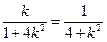
所以
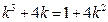 ,即
,即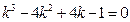 …11分
…11分所以
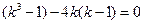
即
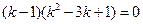
所以
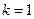 ,或
,或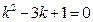 …12分
…12分所以
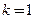 ,或
,或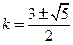 . …13分
. …13分所以这样的直角三角形有三个. …14分
略

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
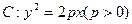 的准线为
的准线为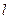 ,焦点为
,焦点为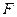 ,圆
,圆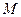 的圆心在
的圆心在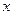 轴的正半轴上,且与
轴的正半轴上,且与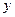 轴相切,过原点
轴相切,过原点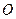 作倾斜角为
作倾斜角为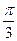 的直线
的直线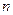 ,交
,交 于点
于点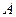 ,交圆
,交圆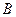 ,且
,且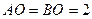
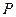 为抛物线C上的动点,求
为抛物线C上的动点,求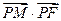 的最小值;
的最小值; 恒过一个定点,并求该定点的坐标.
恒过一个定点,并求该定点的坐标.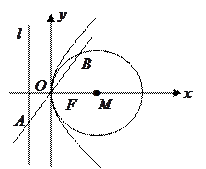
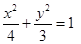 ,则当在此椭圆上存在不同两点关于直线
,则当在此椭圆上存在不同两点关于直线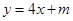 对称时
对称时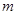 的取值范围为( )
的取值范围为( )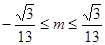
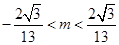
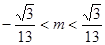
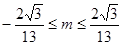
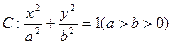 ,其相应于焦点
,其相应于焦点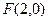 的准线方
的准线方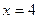 ;
;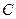 的方程;
的方程;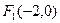 倾斜角为
倾斜角为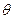 的直线交椭圆
的直线交椭圆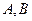 两点,求弦
两点,求弦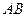 的长度。
的长度。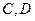 ,求
,求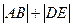
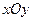 中,已知椭圆
中,已知椭圆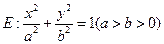 过点
过点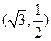 ,且椭圆
,且椭圆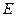 的离心率为
的离心率为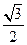 .
.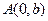 为直角顶点且内接于椭圆
为直角顶点且内接于椭圆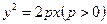 的焦点,斜率为
的焦点,斜率为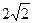 的直线交抛物线于
的直线交抛物线于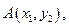
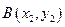 (
(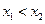 )两点,且
)两点,且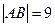
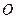 为坐标原点,
为坐标原点,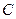 为抛物线上一点,若
为抛物线上一点,若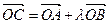 ,求
,求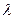 的值
的值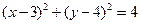
 取得最小值时点P的坐标.
取得最小值时点P的坐标. 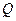 是
是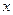 轴上的动点,
轴上的动点,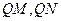 分别切圆
分别切圆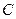 于
于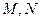 两点
两点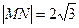 ,求直线
,求直线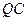 的方程;
的方程;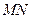 恒过一定点.
恒过一定点.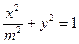 (常数
(常数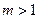 ),P是曲线C上的动点,M是曲线C的右
),P是曲线C上的动点,M是曲线C的右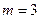 ,求|PA|的最大值与最小值.
,求|PA|的最大值与最小值.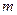 的取值范围.
的取值范围.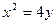 焦点的直线依次交抛物线与圆
焦点的直线依次交抛物线与圆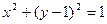 于点A、B、C、D,则
于点A、B、C、D,则 的值是_____
的值是_____