题目内容
11.设x1,x2是函数f(x)=$\frac{1}{3}{x^3}+\frac{1}{2}a{x^2}$+2bx的两个极值点,且x1∈(0,1),x2∈(1,2),则$\frac{b-2}{a+2}$的取值范围是( )| A. | (-2,1) | B. | (-∞,$\frac{1}{4}$)∪(1,+∞) | C. | ($\frac{1}{4}$,1) | D. | (-∞,-2)∪(1,+∞) |
分析 求导函数,利用f(x)的两个极值点分别是x1,x2,x1∈(0,1),x2∈(1,2),建立不等式,利用平面区域,即可求$\frac{b-2}{a+2}$的取值范围.
解答 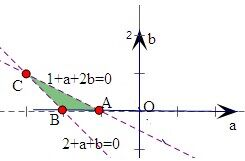 解:由题意,f′(x)=x2+ax+2b.
解:由题意,f′(x)=x2+ax+2b.
∵f(x)的两个极值点分别是x1,x2,x1∈(0,1),
x2∈(1,2),
∴$\left\{\begin{array}{l}{f′(0)=2b>0}\\{f′(1)=1+a+2b<0}\\{f′(2)=4+2a+2b>0}\end{array}\right.$,
对应的平面区域如图所示,三个顶点坐标为A(-1,0),
B(-2,0),C(-3,1),则
在(-1,0)处,$\frac{b-2}{a+2}$=-2,在(-3,1)处,$\frac{b-2}{a+2}$=1,
∴$\frac{b-2}{a+2}$的取值范围是(-∞,-2)∪(1,+∞).
故选:D.
点评 本题考查导数知识的运用:求极值,考查平面区域的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
1.在下列A到B的四种对应关系中,能构成A到B的映射关系的是( )


| A. | (1)(4) | B. | (2)(3) | C. | (2)(4) | D. | (1)(3) |
19.“m∈(-∞,-2)”是“方程$\frac{{x}^{2}}{m-5}$+$\frac{{y}^{2}}{{m}^{2}-m-6}$=1表示的图形为双曲线”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
6.若偶函数f(x)在(-∞,-1]上是增函数,则下列关系式中成立的是( )
| A. | $f(2)<f(-\frac{3}{2})<f(-1)$ | B. | $f(-1)<f(-\frac{3}{2})<f(2)$ | C. | $f(2)<f(-1)<f(-\frac{3}{2})$ | D. | $f(-\frac{3}{2})<f(-1)<f(2)$ |
16.函数$y=sin(2x-\frac{π}{12})cos(2x-\frac{π}{12})$的最小正周期为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |