题目内容
1．在下列A到B的四种对应关系中，能构成A到B的映射关系的是（ ）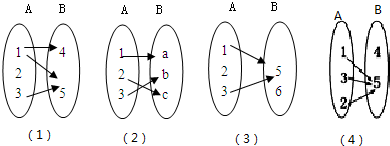
| A． | （1）（4） | B． | （2）（3） | C． | （2）（4） | D． | （1）（3） |
分析 由条件根据映射的定义，判断各个选项中的对应是否能够成映射，从而得出结论．
解答 解：由条件根据映射的定义，A中的每一个元素在B中都有唯一确定的一个元素与之对应，
故只有（2）和（4）能够成映射，
故选：C．
点评 本题主要考查映射的定义，术语基础题．
练习册系列答案
相关题目
9．已知定义在R上的可导函数f（x）的导函数为f′（x），满足f′（x）＜f（x），且f（x+1）=f（-x+3），f（4）=1，则不等式f（x）＜ex的解集为（ ）
| A． | （-∞，e4） | B． | （e4，+∞） | C． | （-∞，0） | D． | （0，+∞） |
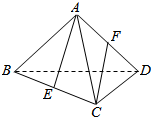如图，在正四面体ABCD中，点E为BC中点，点F为AD中点，则异面直线AE与CF所成角的余弦值为$\frac{2}{3}$．
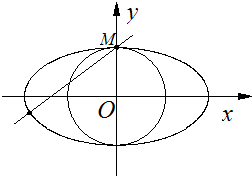如图，圆O与离心率为$\frac{{\sqrt{3}}}{2}$的椭圆T：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）相切于点M（0，1）．
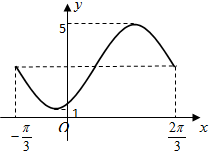已知函数f（x）=Asin（ωx+φ）+h（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象如图所示．
11．设x1，x2是函数f（x）=$\frac{1}{3}{x^3}+\frac{1}{2}a{x^2}$+2bx的两个极值点，且x1∈（0，1），x2∈（1，2），则$\frac{b-2}{a+2}$的取值范围是（ ）
| A． | （-2，1） | B． | （-∞，$\frac{1}{4}$）∪（1，+∞） | C． | （$\frac{1}{4}$，1） | D． | （-∞，-2）∪（1，+∞） |