Question

【题目】已知抛物线y2=2px(p>0)的焦点为F,抛物线上的两个动点A,B始终满足∠AFB=60°,过弦AB的中点H作抛物线的准线的垂线HN,垂足为N,则的取值范围为

A.(0,]B.[,+∞)

C.[1,+∞)D.(0,1]

Answer 1

【答案】D

【解析】

过A，B分别作抛物线准线的垂线AQ，BP，垂足分别为Q，P．设|AF|=a，|BF|=b，根据抛物线的定义得到|HN|=，在中，由余弦定理得，于是得到的表达式，然后根据基本不等式可得所求的范围．

过A，B分别作抛物线准线的垂线AQ，BP，垂足分别为Q，P．

设|AF|=a，|BF|=b，

则由抛物线的定义得|AQ|=a，|BP|=b，

所以|HN|=．

在中，由余弦定理得|AB|2=a2+b2-2abcos 60°=a2+b2-ab，

所以，

因为a+b≥2，

所以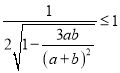，当且仅当a=b时等号成立，

故的取值范围为(0,1]．

故选D．