题目内容
【题目】已知单调递增的等比数列
满足
,且
是
的等差中项.
(Ⅰ)求数列
的通项公式；
(Ⅱ)若
,对任意正数数
， 
恒成立，试求
的取值范围.
【答案】（1）
（2）
【解析】试题分析：(Ⅰ)通过
是
的等差中项可知
，结合
，可知
，进而通过解方程
，可知公比
，从而可得数列
的通项公式；(Ⅱ)通过(Ⅰ) 
，利用错位相减法求得
，对任意正整数
恒成立等价于
对任意正整数
恒成立，问题转化为求
的最小值，从而可得
的取值范围.
试题解析：(Ⅰ)设等比数列
的首项为
,公比为
依题意，有
,
代入
,得
，因此
,
即有
解得
或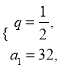
又数列
单调递增，则
故
.
(Ⅱ) 
①
②
①-②，得
对任意正整数
恒成立.
对任意正整数
恒成立，即
恒成立，
,即
的取值范围是
.
【易错点晴】本题主要考查等差数列的通项公式以及求和公式、“错位相减法”求数列的和，以及不等式恒成立问题，属于难题. “错位相减法”求数列的和是重点也是难点，利用“错位相减法”求数列的和应注意以下几点：①掌握运用“错位相减法”求数列的和的条件（一个等差数列与一个等比数列的积）；②相减时注意最后一项 的符号；③求和时注意项数别出错；④最后结果一定不能忘记等式两边同时除以
.
练习册系列答案
中考解读考点精练系列答案
相关题目
【题目】某学校高三年级有学生1 000名，经调查，其中750名同学经常参加体育锻炼(称为A类同学)，另外250名同学不经常参加体育锻炼(称为B类同学)，现用分层抽样方法(按A类、B类分两层)从该年级的学生中共抽查100名同学，如果以身高达165 cm作为达标的标准，对抽取的100名学生，得到以下列联表：
身高达标 | 身高不达标 | 总计 | |
经常参加体育锻炼 | 40 | ||
不经常参加体育锻炼 | 15 | ||
总计 | 100 |
（1）完成上表；
（2）能否在犯错误的概率不超过0.05的前提下认为经常参加体育锻炼与身高达标有关系(K2的观测值精确到0.001)?
