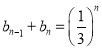题目内容
【题目】已知椭圆![]() 的左焦点
的左焦点![]() ,直线
,直线![]() 与y轴交于点P.且与椭圆交于A,B两点.A为椭圆的右顶点,B在x轴上的射影恰为
与y轴交于点P.且与椭圆交于A,B两点.A为椭圆的右顶点,B在x轴上的射影恰为![]() 。
。
(1)求椭圆E的方程;
(2)M为椭圆E在第一象限部分上一点,直线MP与椭圆交于另一点N,若![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(2)利用已知条件列出方程组,求解椭圆的几何量,然后求解椭圆E的方程.
(2)利用三角形的面积的比值,推出线段的比值,得到![]() .
.
设MN方程:![]() ,
,![]() ,联立方程,利用韦达定理,求出
,联立方程,利用韦达定理,求出![]() ,解出
,解出![]() ,将
,将![]() 代入韦达定理,然后求解实数λ的取值范围.
代入韦达定理,然后求解实数λ的取值范围.
解:![]() 与椭圆的一个交点A为椭圆的右顶点
与椭圆的一个交点A为椭圆的右顶点
![]() .
.
又![]() 轴,得到点
轴,得到点![]() ,
,
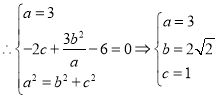 ,
,
椭圆E的方程为![]() 。
。
(2)因为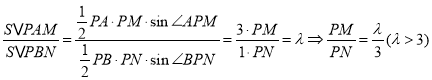
所以![]() ,由(1)可知
,由(1)可知![]() ,设MN方程
,设MN方程![]() ,
,![]() ,
,
联立方程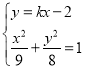 ,得
,得![]() ,得
,得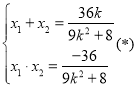 ,
,
又![]() ,有
,有![]() ,将其代入
,将其代入![]() 化简可得:
化简可得:![]() ,因为M为椭圆E在第一象限部分上一点,所以
,因为M为椭圆E在第一象限部分上一点,所以![]() ,
,
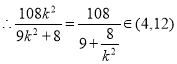 ,则
,则![]() 且
且![]() ,
,
解得![]()

练习册系列答案
 启东小题作业本系列答案
启东小题作业本系列答案
相关题目