题目内容
14.已知函数f(x)=a(x-1)2+lnx,a∈R.(Ⅰ)当a=-$\frac{1}{4}$时,求函数y=f(x)的单调区间;
(Ⅱ)a=$\frac{1}{2}$时,令h(x)=f(x)-3lnx+x-$\frac{1}{2}$.求h(x)在[1,e]上的最大值和最小值;
(Ⅲ)若函数f(x)≤x-1对?x∈[1,+∞)恒成立,求实数a的取值范围.
分析 (Ⅰ)先求导,根据导数和函数的单调性即可求出单调区间;
(Ⅱ)先求导,根据导数和函数的最值的关系即可求出;
(Ⅲ)构造函数,转化为设g(x)=a(x-1)2+lnx-x+1,x∈[1,+∞),则g(x)max≤0,x∈[1,+∞),根据导数和函数最值的关系分类讨论即可.
解答 解:(Ⅰ)当a=-$\frac{1}{4}$时,f(x)=-$\frac{1}{4}$(x-1)2+lnx,(x>0)…(1分)
f'(x)=-$\frac{1}{2}$x+$\frac{1}{2}$+$\frac{1}{x}$=-$\frac{(x-2)(x+1)}{2x}$,…(2分)
①当0<x<2时,f'(x)>0,f(x)在(0,2)单调递增;
②当x>2时,f'(x)<0,f(x)在(2,+∞)单调递减;
所以函数的单调递增区间是(0,2),单调递减区间是(2,+∞).…(4分)
(Ⅱ)当a=$\frac{1}{2}$时,h(x)=f(x)-3lnx+x-$\frac{1}{2}$=$\frac{1}{2}$x2-2lnx,
∴h′(x)=x-$\frac{2}{x}$
令h′(x)=0解得x=$\sqrt{2}$,…(5分)
当x∈[1,$\sqrt{2}$]时,h′(x)<0,当x∈[$\sqrt{2}$,e)时,h′(x)>0,
故x=$\sqrt{2}$是函数h(x)在[1,e]上唯一的极小值点,…(6分)
故h(x)min=h($\sqrt{2}$)=1-ln2,
又h(1)=$\frac{1}{2}$,h(e)=$\frac{1}{2}$e2-2$>\frac{1}{2}$,
所以h(x)max=$\frac{1}{2}$e2-2.…(8分)
(Ⅲ)由题意得a(x-1)2+lnx≤x-1对x∈[1,+∞)恒成立,…(9分)
设g(x)=a(x-1)2+lnx-x+1,x∈[1,+∞),则g(x)max≤0,x∈[1,+∞),
∴$g'(x)=\frac{{2a{x^2}-(2a+1)x+1}}{x}=\frac{(2ax-1)(x-1)}{x}$,…(10分)
①当a≤0时,若x>1,则g′(x)<0,所以g(x)在[1,+∞)单调递减,
∴g(x)max=g(1)=0≤0成立,得a≤0;…(11分)
②当$a≥\frac{1}{2}$时,$x=\frac{1}{2a}≤1$,g(x)在[1,+∞)单调递增,
所以存在x>1,使g(x)>g(1)=0,则不成立;…(12分)
③当$0<a<\frac{1}{2}$时,x=$\frac{1}{2a}$>1,则f(x)在[1,$\frac{1}{2a}$]上单调递减,[$\frac{1}{2a}$,+∞)单调递增,
则存在$\frac{1}{a}$∈[$\frac{1}{2a}$,+∞),有g($\frac{1}{a}$)=a($\frac{1}{a}$-1)2+ln$\frac{1}{a}$-$\frac{1}{a}$+1=-lna+a-1>0,
所以不成立,…(13分)
综上得a≤0.…(14分)
点评 本题考查了导数和函数的单调性,极值,最值的关系,以及函数恒成立的问题,培养学生的转化能力,运算能力,属于难题.

 互动英语系列答案
互动英语系列答案| A. | (2,+∞) | B. | (-∞,-2) | C. | [2,+∞) | D. | (-∞,-2] |
| A. | 若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,则$\overrightarrow{a}$=$\overrightarrow{b}$ | B. | 若λ$\overrightarrow{a}$=0,则λ=0 | C. | 若$\overrightarrow{a}$•$\overrightarrow{c}$=$\overrightarrow{b}$•$\overrightarrow{c}$,则$\overrightarrow{a}$=$\overrightarrow{b}$ | D. | 若$\overrightarrow{a}$=$\overrightarrow{b}$,则$\overrightarrow{a}$•$\overrightarrow{c}$=$\overrightarrow{b}$•$\overrightarrow{c}$ |
| A. | 1 | B. | 3 | C. | 2-$\sqrt{3}$ | D. | 4-$\sqrt{3}$ |
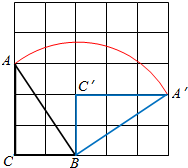 如图,△ABC的3个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点B顺时针旋转到△A′BC′的位置,且点A′、C′仍落在格点上,则线段AB扫过的图形面积是$\frac{13}{4}π$平方单位.
如图,△ABC的3个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点B顺时针旋转到△A′BC′的位置,且点A′、C′仍落在格点上,则线段AB扫过的图形面积是$\frac{13}{4}π$平方单位.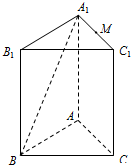 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC.