如图.△ABC的3个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上.将△ABC绕点B顺时针旋转到△A′BC′的位置.且点A′.C′仍落在格点上.则线段AB扫过的图形面积是$\frac{13}{4}π$平方单位．题目和参考答案——青夏教育精英家教网—

题目内容

4．

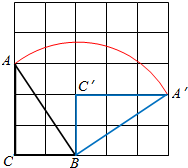如图，△ABC的3个顶点都在5×5的网格（每个小正方形的边长均为1个单位长度）的格点上，将△ABC绕点B顺时针旋转到△A′BC′的位置，且点A′、C′仍落在格点上，则线段AB扫过的图形面积是$\frac{13}{4}π$平方单位．

分析在直角△ABC中，利用勾股定理求出线段AB的长度，代入扇形面积公式，可得线段AB扫过的图形面积．

解答解：直角△ABC中，AC=3，BC=2，
故AB=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$，
线段AB扫过的图形是一个以AB为半径r，圆心角为：α=$\frac{π}{2}$的扇形，
故面积S=$\frac{1}{2}{αr}^{2}$=$\frac{13}{4}π$，
故答案为：$\frac{13}{4}π$．

点评本题考查的知识点是勾股定理和扇形面积公式，难度不大，属于基础题．

练习册系列答案

相关题目

	A．	f（x）=lnx²与g（x）=2lnx是同一个函数		B．	$cos\frac{π}{12}=\frac{{\sqrt{6}-\sqrt{2}}}{4}$
	C．	△ABC中，$cos（A+B）+sin\frac{C}{2}$的最小值是-1		D．	因为$\sqrt{2}=2cos\frac{π}{4}$，所以$\sqrt{2+\sqrt{2}}=2cos\frac{π}{8}$

15．函数f（x）=x³-3x在点（1，-2）处的切线斜率是0．

12．确定结论“X与Y有关系”的可信度为99.5%时，则随即变量k²的观测值k必须（　　）

19．设O为△ABC的外心（三角形外接圆的心），若$\overrightarrow{AO}$•$\overrightarrow{BC}$=$\frac{1}{2}$|$\overrightarrow{AB}$|²，则$\frac{AC}{AB}$=（　　）

A．